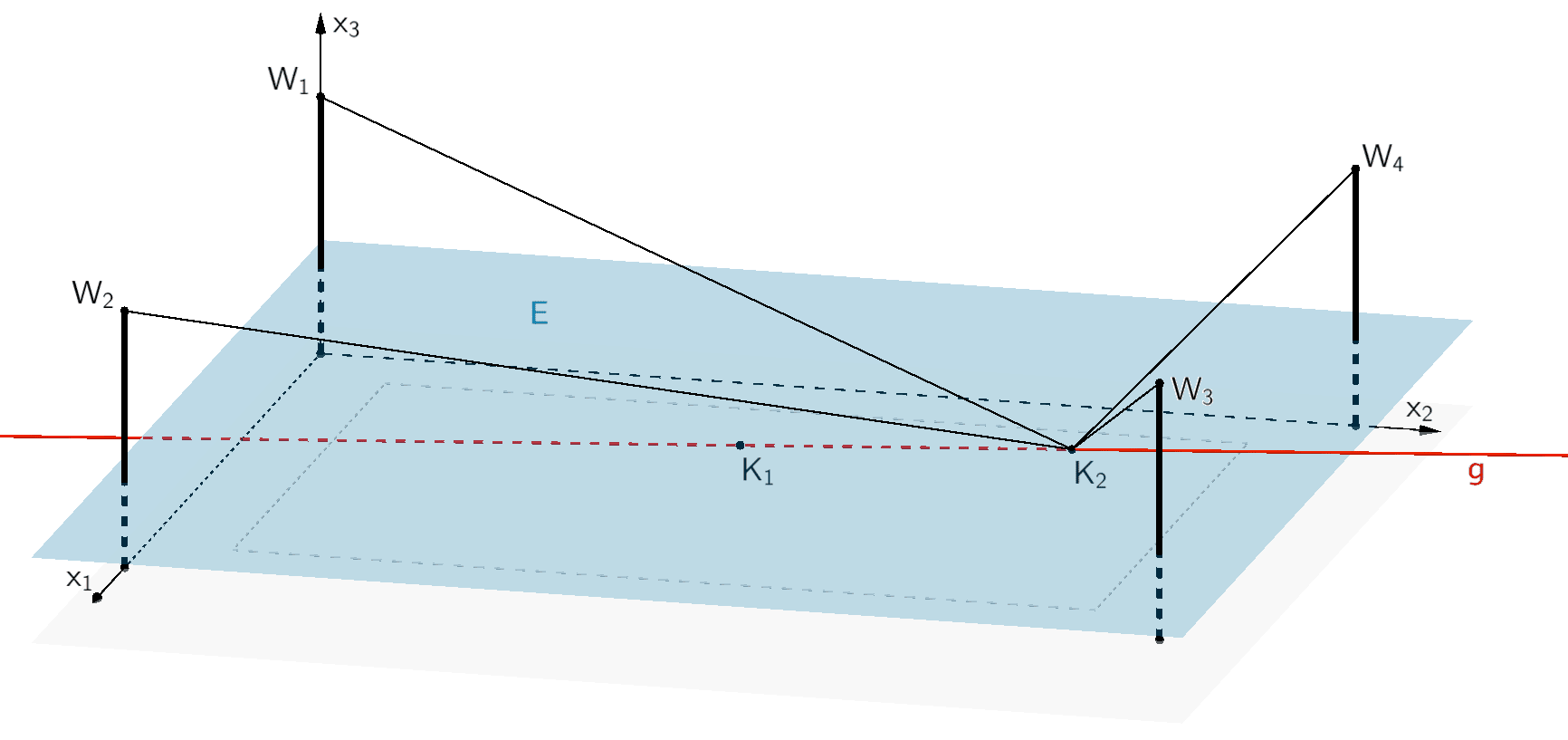
Kurze Zeit später legt sich ein Torhüter den Ball für einen Abstoß bereit. Der Abstoß soll von der Kamera aufgenommen werden. Durch das gleichzeitige Verlängern beziehungsweise Verkürzen der vier Seile wird die Kamera entlang einer geraden Bahn zu einem Zielpunkt bewegt, der in einer Höhe von 10 m über dem Spielfeld liegt. Im Modell wird der Zielpunkt durch den Punkt \(K_{2}\) beschrieben, die Bewegung der Kamera erfolgt vom Punkt \(K_{1}\) entlang der Geraden mit der Gleichung \(g \colon \overrightarrow{X} = \overrightarrow{K_{1}} + \lambda \cdot \begin{pmatrix} 3 \\ 20 \\ 2 \end{pmatrix}, \, \lambda \in \mathbb R\), zum Punkt \(K_{2}\).
Bestimmen Sie die Koordinaten von \(K_{2}\).
(Ergebnis: \(K_{2}(51|100|10)\))
(3 BE)
Lösung zu Teilaufgabe b
Punkt auf einer Geraden, Schnittpunkt Gerade - Ebene
\[g \colon \overrightarrow{X} = \overrightarrow{K_{1}} + \lambda \cdot \begin{pmatrix} 3 \\ 20 \\ 2 \end{pmatrix}, \; \lambda \in \mathbb R\]
\(K_{1}(45|60|6)\) (vgl. Teilaufgabe a)
Der Zielpunkt \(K_{2}\) der Kamera liegt in einer Höhe von 10 m.
\[\Longrightarrow \quad K_{2}(x_{1}|x_{2}|10)\]
Da sich die Kamera entlang der Geraden \(g\) zum Zielpunkt \(K_{2}\) bewegt gilt:
\[K_{2} \in g \colon \overrightarrow{K_{2}} = \overrightarrow{K_{1}} + \lambda \cdot \begin{pmatrix} 3 \\ 20 \\ 2 \end{pmatrix}\]
Mit \(K_{1}(45|60|6)\) und \(K_{2}(x_{1}|x_{2}|10)\) folgt:
\[K_{2} \in g \colon \begin{pmatrix} x_{1} \\ x_{2} \\ 10 \end{pmatrix} = \begin{pmatrix} 45 \\ 60 \\ 6 \end{pmatrix} + \lambda \cdot \begin{pmatrix} 3 \\ 20 \\ 2 \end{pmatrix}\]
\[\begin{align*}\Longrightarrow \quad 10 &= 6 + 2\lambda & &| - 6 \\[0.8em] 4 &= 2\lambda & &| : 2 \\[0.8em] 2 &= \lambda \end{align*}\]
Parmeterwert \(\lambda = 2\) in die Gleichung der Gerden \(g\) einsetzen:
\[K_{2} \in g \colon \overrightarrow{K_{2}} = \begin{pmatrix} 45 \\ 60 \\ 6 \end{pmatrix} + 2 \cdot \begin{pmatrix} 3 \\ 20 \\ 2 \end{pmatrix} = \begin{pmatrix} 51 \\ 100 \\ 10 \end{pmatrix}\]
\[\Longrightarrow \quad K_{2}(51|100|10)\]
Als Alternative formuliert man die Gleichung einer Ebene \(E\), welche in einer Höhe von 10 m parallel zum Spielfeld liegt, und ermittelt den Schnittpunkt dieser Ebene mit der Geraden \(g\).
\[E \colon x_{3} = 10\]
\[g \colon \overrightarrow{X} = \begin{pmatrix} 45 \\ 60 \\ 6 \end{pmatrix} + \lambda \cdot \begin{pmatrix} 3 \\ 20 \\ 2 \end{pmatrix}, \; \lambda \in \mathbb R\]
\[\begin{align*}E \cap g \colon 6 + 2\lambda &= 10 & &| - 6 \\[0.8em] 2\lambda &= 4 & &| : 2 \\[0.8em] \lambda &= 2 \end{align*}\]
Parmeterwert \(\lambda = 2\) in die Gleichung der Gerden \(g\) einsetzen:
\[K_{2} \in g \colon \overrightarrow{K_{2}} = \begin{pmatrix} 45 \\ 60 \\ 6 \end{pmatrix} + 2 \cdot \begin{pmatrix} 3 \\ 20 \\ 2 \end{pmatrix} = \begin{pmatrix} 51 \\ 100 \\ 10 \end{pmatrix}\]
\[\Longrightarrow \quad K_{2}(51|100|10)\]
Schnittpunkt \(K_{2}\) der Ebene \(E\) und der Geraden \(g\)