Mit einem Lasermessgerät soll ein Verkehrsschild angepeilt werden. Diese Situation wird modellhaft in einem Koordinatensystem dargestellt. Der Ausgangspunkt des Laserstrahls wird durch den Punkt \(P(104|-42|10)\) beschrieben, seine Richtung durch den Vektor \(\begin{pmatrix} -13 \\ 5 \\ 1 \end{pmatrix}\). Das Verkehrsschild wird durch eine Kreisscheibe repräsentiert, die in der \(x_{2}x_{3}\)-Ebene liegt und den Mittelpunkt \(M(0|0|20)\) sowie den Radius 3 hat.
Untersuchen Sie, ob der Laserstrahl auf das Verkehrsschild trifft.
(5 BE)
Lösung zur Aufgabe
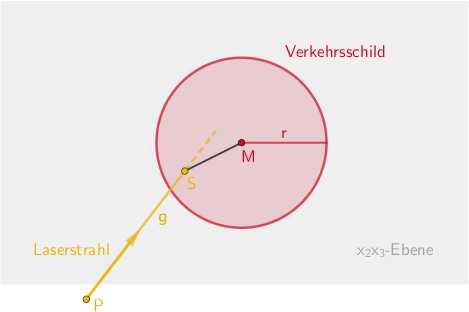
Planskizze (optional): Die Gerade \(\textcolor{#e9b509}{g}\) duch den Punkt \(\textcolor{#e9b509}{P(104|-42|10)}\) und dem Richtungsvektor \(\textcolor{#e9b509}{\begin{pmatrix} -13 \\ 5 \\ 1 \end{pmatrix}}\) beschreibt im Modell den Verlauf des Laserstrahls. Der Kreis mit dem Mittelpunkt \(\textcolor{#cc071e}{M(0|0|20)}\) und dem Radius \(\textcolor{#cc071e}{r = 3}\) repräsentiert das Verkehrsschild, welches in der \(x_{2}x_{3}\)-Ebene liegt.
Die Gerade \(\textcolor{#e9b509}{g}\) (Laserstrahl) schneidet die \(x_{2}x_{3}\)-Ebene im Punkt \(\textcolor{#e9b509}{S}\). Der Laserstrahl trifft auf das Verkehrsschild, wenn der Abstand der Punkte \(\textcolor{#e9b509}{S}\) und \(\textcolor{#cc071e}{M}\) kleiner ist als der Radius des Kreises (Verkehrsschild).
Gleichung der Gerade \(\textcolor{#e9b509}{g}\) und der \(x_{2}x_{3}\)-Ebene formulieren:
Gleichung einer Gerade / Strecke in Parameterform
Jede Gerade \(g\) kann durch eine Gleichung in der sogenannten Parameterform
\(g \colon \overrightarrow{X} = \overrightarrow{A} + \lambda \cdot \overrightarrow{u} \enspace\) mit dem Parameter \(\lambda \in \mathbb R\) beschrieben werden.
Dabei ist \(\overrightarrow{A}\) der Ortsvektor eines Aufpunkts (Stützvektor) und \(\overrightarrow{u}\) ein Richtungsvektor der Gerade \(g\).
Gleichung einer Strecke \([AB]\) in Parameterform:
\[\overrightarrow{X} = \overrightarrow{A} + \lambda \cdot \overrightarrow{AB}, \; \textcolor{#cc071e}{\lambda \in [0;1]} \]
\[\textcolor{#e9b509}{g \colon \overrightarrow{X} = \begin{pmatrix} 104 \\ -42 \\ 10 \end{pmatrix} + \lambda \cdot \begin{pmatrix} -13 \\ 5 \\ 1 \end{pmatrix}, \; \lambda \in \mathbb R}\]
Eine Gleichung der \(x_{2}x_{3}\)-Ebene in Normalenform ist beispielsweise \(x_{1} = 0\).
Schnittpunkt \(\textcolor{#e9b509}{S}\) der Gerade \(\textcolor{#e9b509}{g}\) und der \(x_{2}x_{3}\)-Ebene bestimmen:
Hierfür wird die \(x_{1}\)-Koordinate des Ortsvektors \(\overrightarrow{X}\) der Gleichung von \(\textcolor{#e9b509}{g}\) in die Ebenengleichung \(x_{1} = 0\) der \(x_{2}x_{3}\)-Ebene eingesetzt und diese nach dem Parameter \(\lambda\) aufgelöst.
\[\begin{align*} \textcolor{#e9b509}{g} \cap x_{2}x_{3}\text{-Ebene}\,\colon \textcolor{#e9b509}{104 - 13 \lambda} &= 0 &&| + 13 \lambda \\[0.8em] 104 &= 13\lambda &&| : 13 \\[0.8em] 8 &= \lambda \end{align*}\]
Durch Einsetzen des Parameterwerts \(\lambda = 8\) in die Gleichung der Gerade \(\textcolor{#e9b509}{g}\) erhält man den Ortsvektor des Schnittpunkts \(\textcolor{#e9b509}{S}\).
\[\textcolor{#e9b509}{S \in g \colon \overrightarrow{S}} = \begin{pmatrix} 104 \\ -42 \\ 10 \end{pmatrix} + 8 \cdot \begin{pmatrix} -13 \\ 5 \\ 1 \end{pmatrix} = \textcolor{#e9b509}{\begin{pmatrix} 0 \\ -2 \\ 18 \end{pmatrix}}\]
Abstand der Punkte \(\textcolor{#e9b509}{S}\) und \(\textcolor{#cc071e}{M}\) berechnen und mit dem Radius \(\textcolor{#cc071e}{r = 3}\) vergleichen:
Betrag eines Vektors
\[ \vert \overrightarrow{a} \vert = \sqrt{\overrightarrow{a} \circ \overrightarrow{a}} = \sqrt{{a_1}^2 + {a_2}^2 + {a_3}^2}\]
(vgl. Merkhilfe)
\[\begin{align*} d(\textcolor{#e9b509}{S};\textcolor{#cc071e}{M}) &= \vert \overrightarrow{\textcolor{#e9b509}{S}\textcolor{#cc071e}{M}} \vert = \vert \textcolor{#cc071e}{\overrightarrow{M}} - \textcolor{#e9b509}{\overrightarrow{S}} \vert \\[0.8em] &= \left| \textcolor{#cc071e}{\begin{pmatrix} 0 \\ 0 \\ 20 \end{pmatrix}} - \textcolor{#e9b509}{\begin{pmatrix} 0 \\ -2 \\ 18 \end{pmatrix}} \right| \\[0.8em] &= \left| \begin{pmatrix} 0 \\ 2 \\ 2 \end{pmatrix} \right| = \sqrt{0^{2} + 2^{2} + 2^{2}} = \sqrt{8}\end{align*}\]
Da \(\sqrt{8} < \textcolor{#cc071e}{3} \; (= \textcolor{#cc071e}{\sqrt{9}})\) gilt, trifft der Laserstrahl auf das Verkehrsschild.
Alternativer Vergleich mit dem Radius des Kreises:
Zunächst wird die Gleichung des Kreises \(\textcolor{#cc071e}{k}\) in der \(x_{2}x_{3}\)-Ebene mit dem Mittelpunkt \(\textcolor{#cc071e}{M(0|0|20)}\) und dem Radius \(\textcolor{#cc071e}{r = 3}\) formuliert. Anschließend lässt sich mithilfe einer Punktprobe prüfen, ob der Punkt \(\textcolor{#e9b509}{S(0|-2|18)}\) innerhalb des Kreises liegt.
Kreisgleichung (Kreis in einer Koordinatenebene)
Ein Kreis mit dem Mittelpunkt \(M(m_{1}|m_{2})\) und dem Radius \(r\) wird in der \(x_{1}x_{2}\)-Ebene beschrieben durch:
Vektordarstellung
\[(\overrightarrow{X} - \overrightarrow{M})^{2} = r^{2}\]
Koordinatendarstellung
\[(x_{1} - m_{1})^{2} + (x_{2} - m_{2})^{2} = r^{2}\]
Die Gleichungen gelten analog für die \(x_{1}x_{3}\)- bzw. die \(x_{2}x_{3}\)-Ebene.
\[\begin{align*}\textcolor{#cc071e}{k} \colon (x_{2} - \textcolor{#cc071e}{m_{2}})^{2} + (x_{3} - \textcolor{#cc071e}{m_{3}})^{2} &= \textcolor{#cc071e}{r}^{2} \\[0.8em] \textcolor{#cc071e}{k} \colon (x_{2} - \textcolor{#cc071e}{0})^{2} + (x_{3} - \textcolor{#cc071e}{20})^{2} &= \textcolor{#cc071e}{3}^{2} \\[0.8em] \textcolor{#cc071e}{k} \colon x_{2}^{2} + (x_{3} - \textcolor{#cc071e}{20})^{2} &= \textcolor{#cc071e}{3}^{2}\end{align*}\]
Punktprobe \(\textcolor{#e9b509}{S(0|-2|18)}\) in \(\textcolor{#cc071e}{k}\):
\[\begin{align*} (\textcolor{#e9b509}{-2})^{2} + (\textcolor{#e9b509}{18} - \textcolor{#cc071e}{20})^{2} &\overset{?}{=} \textcolor{#cc071e}{3}^{2} \\[0.8em] \Rightarrow \enspace (-2)^{2} + (-2)^{2} &< \textcolor{#cc071e}{9} \\[0.8em] 8 &< \textcolor{#cc071e}{9} \end{align*}\]
MIt \(8 < \textcolor{#cc071e}{9}\) liegt der Punkt \(\textcolor{#e9b509}{S}\) innerhalb des Kreises \(\textcolor{#cc071e}{k}\). Folglich trifft der Laserstrahl auf das Verkehrsschild.


