Genau eine der folgenden Gleichungen (1) bis (3) beschreibt eine Symmetrieebene der Pyramide. Geben Sie diese Gleichung an und begründen Sie für eine der anderen Gleichungen, dass die durch sie beschriebene Ebene keine Symmetrieebene der Pyramide ist.
\[\textsf{(1)} \quad x_1-x_3=0\]
\[\textsf{(2)} \quad x_1+x_2+x_3=4\]
\[\textsf{(3)} \quad x_1+x_2= 0\]
(3 BE)
Lösung zu Teilaufgabe b
Gleichung (3) beschreibt eine Symmetrieebene der Pyramide.
Gleichung (1) beschreibt keine Symmetrieebene der Pyramide, da sie nicht den Punkt \(S(0|0|4)\) enthält.
oder
Gleichung (2) beschreibt keine Symmetrieebene der Pyramide, da sie nicht den Koordinatenursprung \(O(0|0|0)\) enthält.
Ergänzende Erklärung (nicht verlangt)

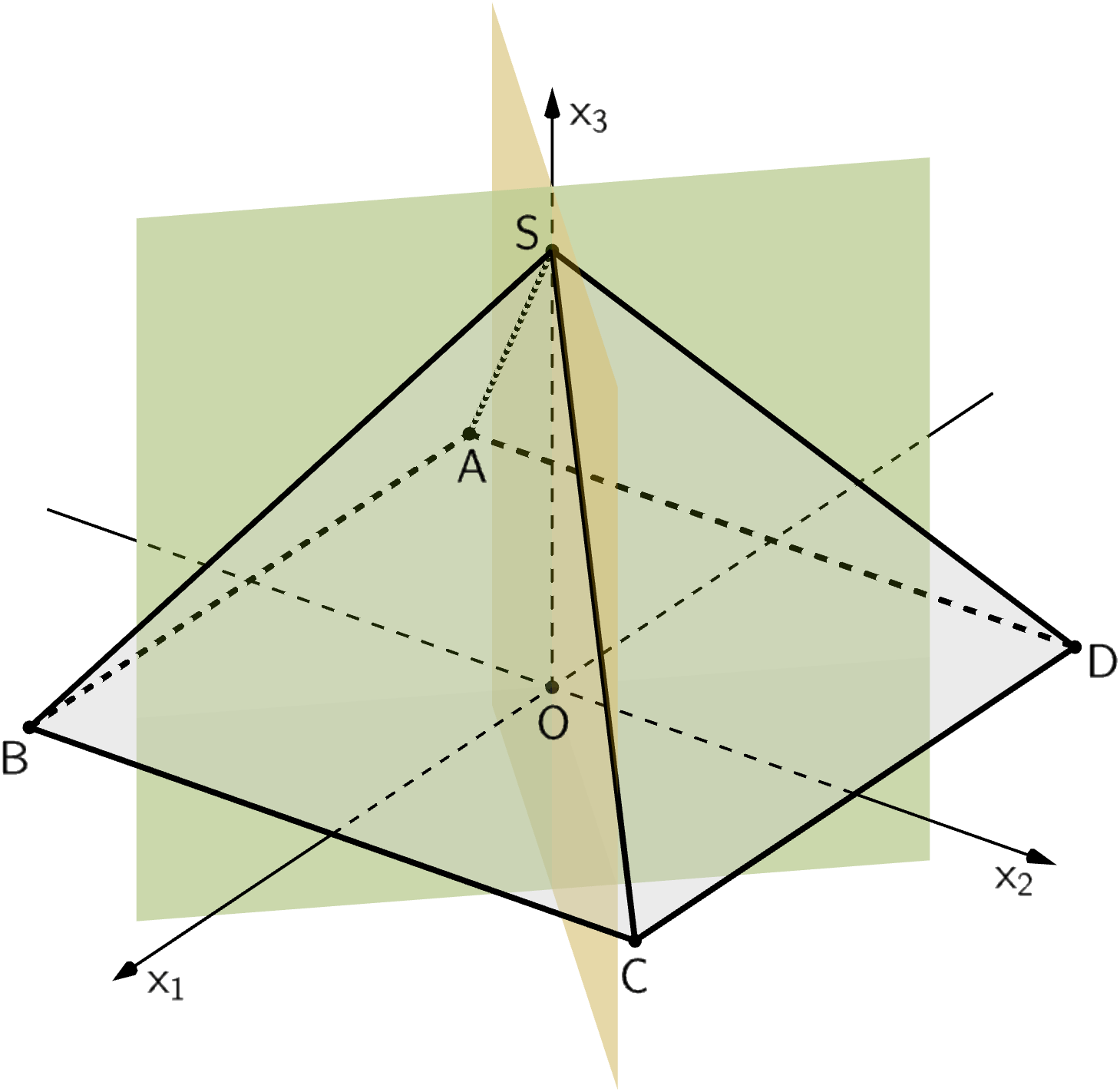
Alle Symmetrieebenen der Pyramide \(ABCDS\) enthalten die \(x_3\)-Achse und somit die Punkte \(O(0|0|0)\) und \(S(0|0|4)\).
\[\textsf{(1)} \quad x_1-x_3=0\]
Punktprobe mit \(O(0|0|0)\):
\[0 - 0 = 0\quad (\textcolor{#89ba17}{\text{w}})\]
Punktprobe mit \(S(0|0|4)\):
\[0 - 4 = 0 \quad (\textcolor{#cc071e}{\text{f}})\]
\(\Rightarrow\) keine Symmetrieebene
\[\textsf{(2)} \quad x_1+x_2+x_3=4\]
Punktprobe mit \(O(0|0|0)\):
\[0 + 0 + 0 = 4\quad (\textcolor{#cc071e}{\text{f}})\]
Punktprobe mit \(S(0|0|4)\):
\[0 + 0 + 4 = 4 \quad (\textcolor{#89ba17}{\text{w}})\]
\(\Rightarrow\) keine Symmetrieebene
\[\textsf{(3)} \quad x_1+x_2= 0\]
Punktprobe mit \(O(0|0|0)\):
\[0 + 0 = 0\quad (\textcolor{#89ba17}{\text{w}})\]
Punktprobe mit \(S(0|0|4)\):
\[0 + 0 = 0 \quad (\textcolor{#89ba17}{\text{w}})\]
\(\Rightarrow\) Symmetrieebene der Pyramide


