Ein Solarmodul wird an einem Metallrohr befestigt, das auf einer horizontalen Fläche senkrecht steht. Das Solarmodul wird modellhaft durch das Rechteck \(ABCD\) dargestellt. Das Metallrohr lässt sich durch eine Strecke, der Befestigungspunkt am Solarmodul durch den Punkt \(M\) beschreiben (vgl. Abbildung). Die horizontale Fläche liegt im Modell in der \(x_{1}x_{2}\)-Ebene des Koordinatensystems; eine Längeneinheit entspricht 0,8 m in der Realität.
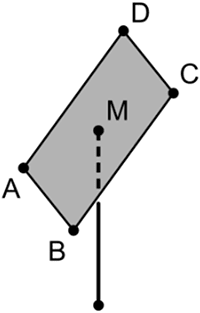
Um einen möglichst großen Energieertrag zu erzielen, sollte die Größe des Neigungswinkels \(\varphi\) des Solarmoduls gegenüber der Horizontalen zwischen 30° und 36° liegen. Prüfen Sie, ob diese Bedingung erfüllt ist.
(3 BE)
Lösung zu Teilaufgabe d
Schnittwinkel zweier Ebenen
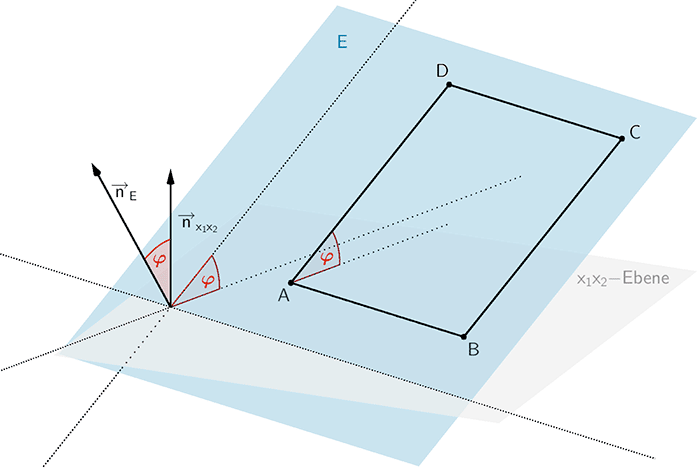
Der Neigungswinkel \(\varphi\) des Solarmoduls (Viereck \(ABCD\)) gegenüber der Horizontalen entspricht dem Schnittwinkel der Ebene \(E\) und der \(x_{1}x_{2}\)-Ebene.
Der Schnittwinkel der Ebenen \(E\) und der \(x_{1}x_{2}\)-Ebene ist der spitze Winkel zwischen zwei Geraden, welche in demselben Punkt auf der Schnittgerade senkrecht stehen und in der Ebene \(E\) bzw. in der \(x_{1}x_{2}\)-Ebene liegen.
Dieser Schnittwinkel ist gleich dem spitzen Winkel, den die Normalenvektoren \(\overrightarrow{n}_{E}\) und \(\overrightarrow{n}_{x_{1}x_{2}}\) festlegen.
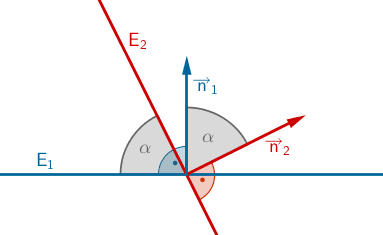
Schnittwinkel \(\boldsymbol{\alpha}\) zweier Ebenen
\[E_1\colon \enspace \overrightarrow{n}_1 \circ \left( \overrightarrow{X} - \overrightarrow{A} \right) = 0\]
\[E_2\colon \enspace \overrightarrow{n}_2 \circ \left( \overrightarrow{X} - \overrightarrow{B} \right) = 0\]
\[\cos \alpha = \frac{\vert \overrightarrow{n}_1 \circ \overrightarrow{n}_2 \vert}{\vert \overrightarrow{n}_1 \vert \cdot \vert \overrightarrow{n}_2 \vert} \enspace \Rightarrow \enspace \alpha = \cos^{-1}(\dots)\]
\[(0^{\circ} \leq \alpha \leq 90^{\circ})\]
Aus Teilaufgabe 1c ist ein Normalenvektor \(\overrightarrow{n}_{E}\) der Ebene \(E\) bekannt. Er kann auch dem möglichen Ergebnis der Ebenengleichung von \(E\) entnommen werden.
\[E \colon 3x_{1} - x_{2} + 5x_{3} - 5 = 0 \quad \Longrightarrow \quad \overrightarrow{n}_{E} = \begin{pmatrix} 3 \\ -1 \\ 5 \end{pmatrix}\]
Ein Normalenvektor der \(x_{1}x_{2}\)-Ebene ist beispielsweise \(\overrightarrow{n}_{x_{1}x_{2}} = \begin{pmatrix} 0 \\ 0 \\ 1 \end{pmatrix}\).
Skalarprodukt
Unter dem Skalarprodukt \(\overrightarrow{a} \circ \overrightarrow{b}\) zweier Vektoren \(\overrightarrow{a}\) und \(\overrightarrow{b}\) versteht man das Produkt aus den Beträgen der beiden Vektoren und dem Kosinus des von den Vektoren eingeschlossenen Winkels \(\varphi\).
\[\overrightarrow{a} \circ \overrightarrow{b} = \vert \overrightarrow{a} \vert \cdot \vert \overrightarrow{b} \vert \cdot \cos{\varphi} \quad (0^{\circ} \leq \varphi \leq 180^{\circ})\]
Berechnung eines Skalarprodukts im \(\boldsymbol{\mathbb R^{3}}\) (vgl. Merkhilfe)
\[\overrightarrow{a} \circ \overrightarrow{b} = \begin{pmatrix} a_{1} \\ a_{2} \\ a_{3} \end{pmatrix} \circ \begin{pmatrix} b_{1} \\ b_{2} \\ b_{3} \end{pmatrix} = a_{1}b_{1} + a_{2}b_{2} + a_{3}b_{3}\]
Betrag eines Vektors
\[ \vert \overrightarrow{a} \vert = \sqrt{\overrightarrow{a} \circ \overrightarrow{a}} = \sqrt{{a_1}^2 + {a_2}^2 + {a_3}^2}\]
(vgl. Merkhilfe)
\[\begin{align*} \cos \varphi &= \frac{\left| \overrightarrow{n}_{E} \circ \overrightarrow{n}_{x_{1}x_{2}} \right|}{\left| \overrightarrow{n}_{E} \right| \cdot \left| \overrightarrow{n}_{x_{1}x_{2}} \right|} \\[0.8em] &= \frac{\left| \begin{pmatrix} 3 \\ -1 \\ 5 \end{pmatrix} \circ \begin{pmatrix} 0 \\ 0 \\ 1 \end{pmatrix} \right|}{\left| \begin{pmatrix} 3 \\ -1 \\ 5 \end{pmatrix} \right| \cdot \left| \begin{pmatrix} 0 \\ 0 \\ 1 \end{pmatrix} \right|} \\[0.8em] &= \frac{\vert 3 \cdot 0 + (-1) \cdot 0 + 5 \cdot 1 \vert}{\sqrt{3^{2} + (-1)^{2} + 5^{2}} \cdot \sqrt{0^{2} + 0^{2} + 1^{2}}} \\[0.8em] &= \frac{5}{\sqrt{35}} \\[0.8em] &= \frac{\sqrt{35}}{7} & &| \; \text{TR:} \; \cos^{-1}(\dots) \\[3.2em] \varphi &\approx 32{,}31^{\circ}\end{align*}\]
Das Solarmodul ist gegenüber der Horizontalen um ca. 32° geneigt. Die Bedingung für einen möglichst großen Energieertrag ist damit erfüllt.


