Zehn 40- bis 44-jährige Frauen wurden zufällig ausgewählt.
Bestimmen Sie die Wahrscheinlichkeiten folgender Ereignisse:
\(A\,\colon\;\)„Unter ihnen sind genau drei Raucherinnen."
\(B\,\colon\;\)„Unter ihnen sind höchstens vier Raucherinnen."
(4 BE)
Lösung zu Teilaufgabe 3a
Ereignisse:
\(R\): "Raucher"
\(\overline R\): "Nichtraucher"
\(M\): "männlich"
\(W\): "weiblich" (\(W = \overline{M}\))
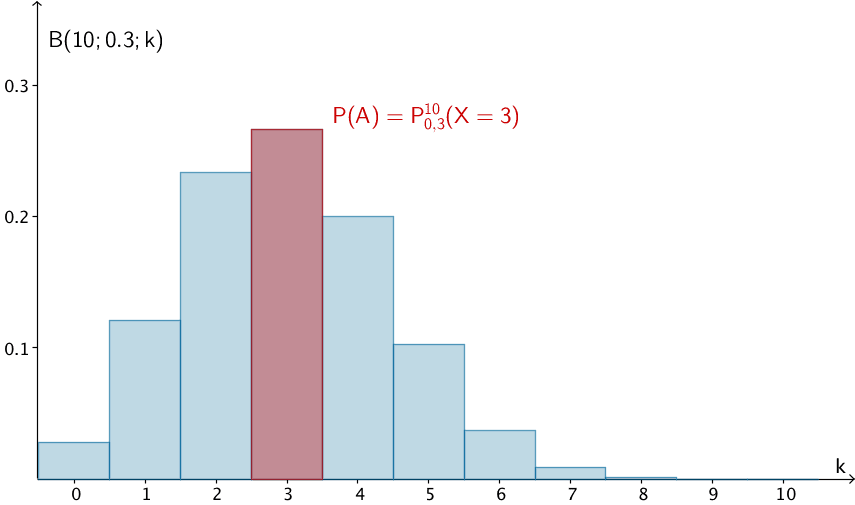
Wahrscheinlichkeit für das Ereignis \(A\): "Unter ihnen sind genau drei Raucherinnen"
Zufallsgröße \(X \colon \enspace\)„Anzahl der 40-44-jährigen Raucherinnen"
Analyse der Angabe:
"Zehn 40-44-jährige Frauen ..."
\[\Longrightarrow \quad n = 10\]
"... genau drei Raucherinnen"
\[\Longrightarrow \quad X = 3\]
Aus dem Diagramm abzulesen:
\[P(40-44, W, R) = 0{,}30\]
Binomialverteilung
Binomialverteilte Zufallsgröße
Für eine Zufallsgröße \(X\), welche bei einer Bernoulli-Kette der Länge \(n\) die Anzahl der Treffer \(k \in \{0,1,\dots,n\}\) mit der Trefferwahrscheinlichkeit \(p\) angibt, gilt:
Binomialverteilung (vgl. Merkhilfe)
\[P_{p}^{n}(X = k) = B(n;p;k) = \binom{n}{k} \cdot p^{k} \cdot (1 - p)^{n - k} \quad (0 \leq k \leq n)\]
Eine Binomialverteilung ist durch die Parameter \(n\) und \(p\) eindeutig bestimmt und wird durch das Symbol \(B(n:p)\) gekennzeichnet. \(X\) heißt binomialverteilt nach \(B(n;p)\).
Voraussetzung für eine Binomialverteilung
Ein Zufallsexperiment, bei dem nur zwei sich gegenseitig ausschließende Ereignisse \(A\) und \(\overline{A}\) mit konstanten Wahrscheinlichkeiten eintreten können (Bernoulli-Experiment).
Die Zufallsgröße \(X\) ist nach \(B(10;0{,}3)\) binomialverteilt.
Stochastisches Tafelwerk (ST) verwenden:
\[P(A) = P^{10}_{0{,}3}(X = 3) = B(10; 0{,}3; 3) \enspace \overset{\text{ST}}{=} \enspace 0{,}26683 \approx 26{,}7 \, \%\]
Alternative: Anwenden der Formel von Bernoulli:
Formel von Bernoulli
Wahrscheinlichkeit für genau \(k\) Treffer bei einer Bernoullikette der Länge \(n\) und der Trefferwahrscheinlichkeit \(p\) für das Eintreten eines betrachteten Ereignisses:
\[P(X = k) = B(n;p;k) = \binom{n}{k} \cdot p^k \cdot (1 - p)^{n - k}\]
\[k \in \{0,1,\dots,n\}\]
\[\begin{align*} P(A) &= P^{10}_{0{,}3}(X =3) = B(10; 0{,}3; 3) \\[0.8em] &= \binom{10}{3} \cdot 0{,}3^3 \cdot (1 - 0{,}3)^{10 - 3} \\[0.8em] &= \binom{10}{3} \cdot 0{,}3^{3} \cdot 0{,}7^{7} \\[0.8em] &\approx 0{,}267 = 26{,}7 \, \% \end{align*}\]
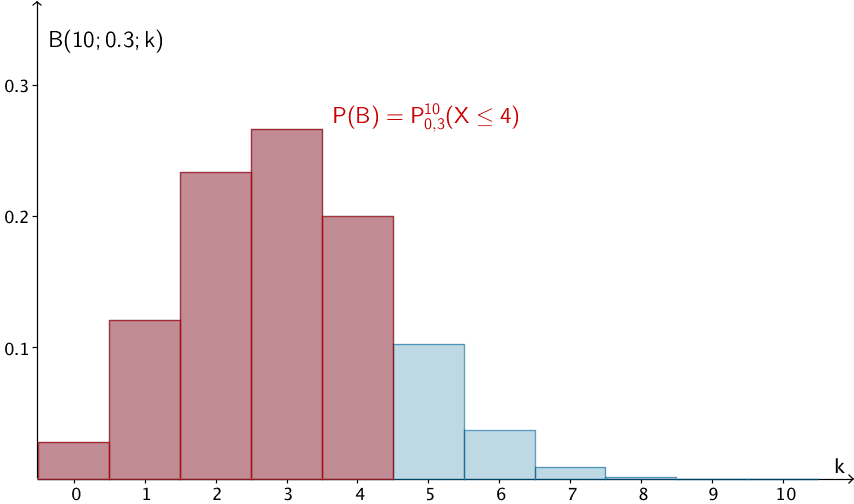
Wahrscheinlichkeit für das Ereignis \(B\): "Unter ihnen sind höchstens vier Raucherinnen"
Zufallsgröße \(X \colon \enspace\)„Anzahl der 40-44-jährigen Raucherinnen"
Analyse der Angabe:
"Zehn 40-44-jährige Frauen ..."
\[\Longrightarrow \quad n = 10\]
"... höchstens vier Raucherinnen"
\[\Longrightarrow \quad X \leq 4\]
Aus dem Diagramm abzulesen:
\[P(40-44, W, R) = 0{,}30\]
Binomialverteilung
Binomialverteilte Zufallsgröße
Für eine Zufallsgröße \(X\), welche bei einer Bernoulli-Kette der Länge \(n\) die Anzahl der Treffer \(k \in \{0,1,\dots,n\}\) mit der Trefferwahrscheinlichkeit \(p\) angibt, gilt:
Binomialverteilung (vgl. Merkhilfe)
\[P_{p}^{n}(X = k) = B(n;p;k) = \binom{n}{k} \cdot p^{k} \cdot (1 - p)^{n - k} \quad (0 \leq k \leq n)\]
Eine Binomialverteilung ist durch die Parameter \(n\) und \(p\) eindeutig bestimmt und wird durch das Symbol \(B(n:p)\) gekennzeichnet. \(X\) heißt binomialverteilt nach \(B(n;p)\).
Voraussetzung für eine Binomialverteilung
Ein Zufallsexperiment, bei dem nur zwei sich gegenseitig ausschließende Ereignisse \(A\) und \(\overline{A}\) mit konstanten Wahrscheinlichkeiten eintreten können (Bernoulli-Experiment).
Die Zufallsgröße \(X\) ist nach \(B(10;0{,}3)\) binomialverteilt.
\[P(B) = P^{10}_{0{,}3}(X \leq 4)\]
Kumulative Verteilungsfunktion einer nach \(B(n, p)\) binomialverteilten Zufallsgröße \(X\)
\[F^n_p (k) = P^n_p (X \leq k) = \sum_{i \, = \, 0}^k B(n; p; i) = \sum_{i \, = \, 0}^k \binom{n}{i} \cdot p^i \cdot (1 - p)^{n - i}\]
Wobei \(n\) die Länge der Bernoullikette, \(p\) die Trefferwahrscheinlichkeit für das Eintreten des betrachteten Ereignisses und \(k \in \{0,1,\dots,n\}\) die Anzahl der Treffer ist.
Das Stochastische Tafelwerk (ST) listet die Werte der Kumulativen Verteilungsfunktion jeweils in der rechten Spalte einer betrachteten Tabelle der Parameter \(n\) und \(p\).
Stochastisches Tafelwerk (ST) verwenden:
\[P(B) = F^{10}_{0{,}3}(4) = P^{10}_{0{,}3}(X \leq 4) = \sum_{i \, = \, 0}^{4} B(10; 0{,}3; i) \enspace \overset{\text{ST}}{=} \enspace 0{,}84973 \approx 85{,}0 \, \%\]