Bestimmen Sie \(\displaystyle \int_1^4 f(t)\,dt\) näherungsweise mithilfe von Abbildung 3. Deuten Sie den Wert des Integrals im Sachzusammenhang.

(5 BE)

Lösung zu Teilaufgabe 2b

Näherungswert für \(\int_1^4 f(t)\,dt\)

Das bestimmte Integral \(\int_1^4 f(t)\,dt\) entspricht dem Flächeninhalt des Flächenstücks, das \(G_f\) für \(t \in [1;4]\) mit der \(x\)-Achse einschließt.

Lösungsansatz 1: Grafische Näherung mithilfe geeigneter Teilflächen

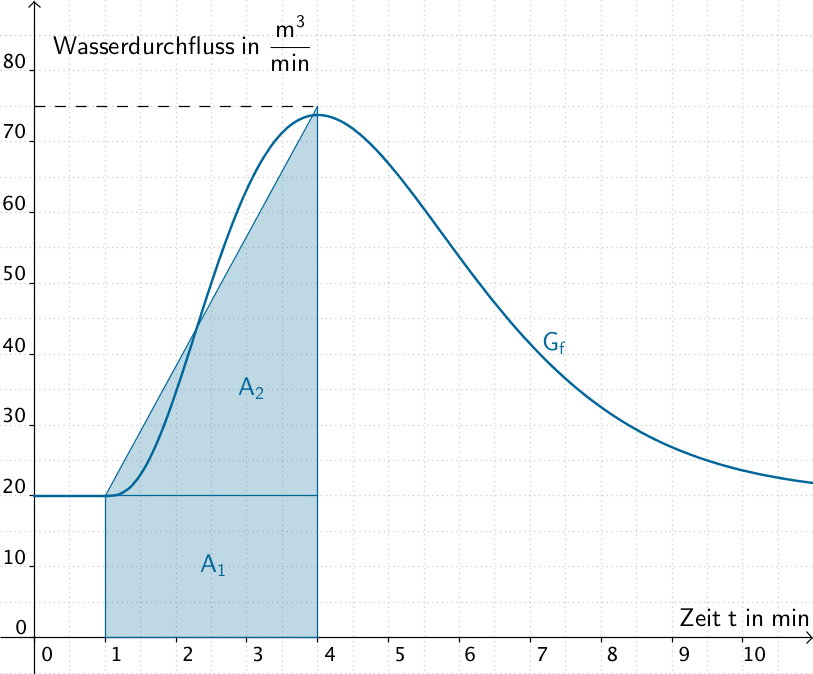
Der Flächeninhalt lässt sich näherungsweise berechnen, indem das Flächenstück in geignete, einfach zu berechnende Teilflächen unterteilt wird.

\[\begin{align*} \int_1^4 f(t)\,dt &\approx A_1 + A_2 \\[0.8em] &= (4 - 1) \;\text{min} \cdot 20 \; \frac{\text{m}^3}{\text{min}} + \frac{1}{2} \cdot (4 - 1) \;\text{min} \cdot (75 - 20) \;\frac{\text{m}^3}{\text{min}} \\[0.8em] &= 142{,}5\;\text{m}^3 \end{align*}\]

Lösungsansatz 2: Grafische Näherung durch "Zählen der Kästchen"

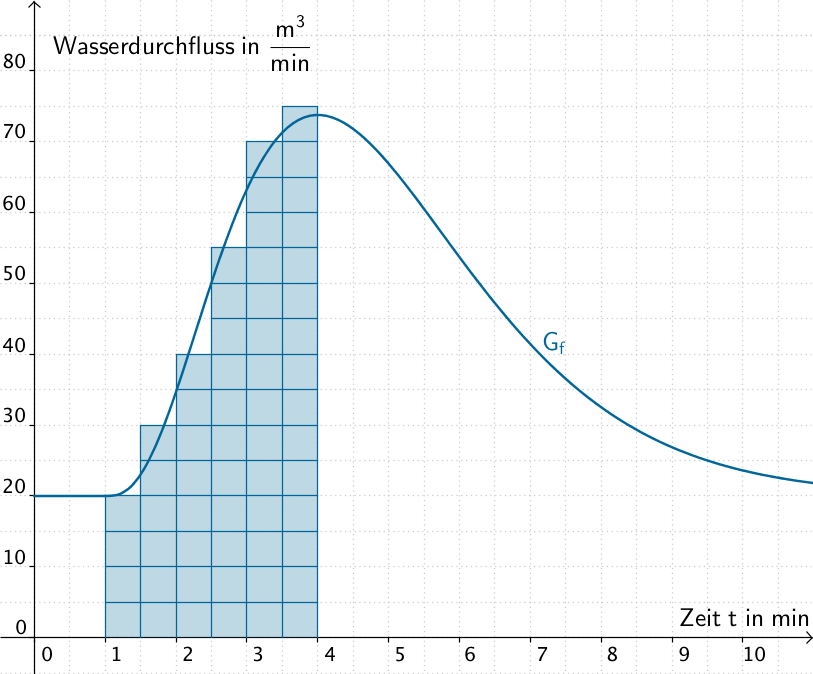
Der Flächeninhalt lässt sich näherungsweise berechnen, indem das Flächenstück in gleich große Kästchen unterteilt wird. In diesem Fall sind es 58 Kästchen.

Betrachtung des Flächeninhalts eines Kästchens:

\[A_{Kästchen} = 0{,}5 \cdot 5 = 2{,}5\]

Der Flächneinhalt eines Kästchen entspricht einer Wassermenge von 2,5 m³.

\[\int_1^4 f(t)\,dt \approx 58 \cdot 2{,}5 \;\text{m}^3 = 145\;\text{m}^3\]

Bedeutung im Sachzusammenhang

Während der drei Minuten ab der ersten bis zur vierten Minute nach dem Öffnen der Schleuse fließen ca. 142,5 m³ bzw. 145 m³ Wasser an der Meßstelle durch.