- Details
- Kategorie: Geometrie 2
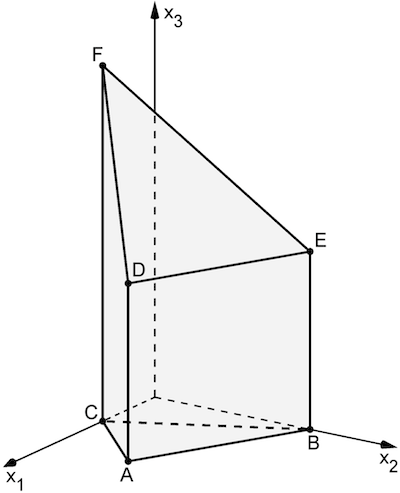
Die Abbildung zeigt den Körper \(ABCDEF\) mit \(A(6|3|0)\), \(B(0|6|0)\), \(C(3|0|0)\), \(D(6|3|6)\), \(E(0|6|6)\) und \(F(3|0|12)\).
Die Punkte \(D\), \(E\) und \(F\) liegen in der Ebene \(L\).
Ermitteln Sie eine Gleichung von \(L\) in Koordinatenform.
(zur Kontrolle: \(2x_1 + 4x_2 + 3x_3 - 42 = 0\))
(4 BE)
- Details
- Kategorie: Geometrie 2
Bestimmen Sie die Größe des Winkels, den \(L\) mit der \(x_1x_2\)-Ebene einschließt.
(3 BE)
- Details
- Kategorie: Geometrie 2
Der Flächeninhalt des Dreiecks \(ABC\) kann mit dem Term \(6 \cdot 6 - \dfrac{1}{2} \cdot 3 \cdot 3 - 2 \cdot \dfrac{1}{2} \cdot 3 \cdot 6\) berechnet werden. Veranschaulichen Sie diese Tatsache durch geeignete Eintragungen in der Abbildung.
(3 BE)
- Details
- Kategorie: Geometrie 2
Die Ebene \(N_k\) enthält die \(x_3\)-Achse und den Punkt \(P_k(1-k|k|0)\) mit \(k \in \; ]0;1[\). Welche Kanten des Körpers von \(N_k\) geschnitten werden, ist abhängig von \(k\). Durchläuft \(k\) alle Werte zwischen \(0\) und \(1\), so gibt es Bereiche \(]a;b[\), für die jeweils gilt, dass \(N_k\) für alle Werte von \(k \in \; ]a;b[\) die gleichen Kanten des Körpers schneidet. Bestimmen Sie den größten dieser Bereiche und geben Sie die zugehörigen Kanten an.
(4 BE)
- Details
- Kategorie: Geometrie 2
Auf der Kante \([AD]\) liegt der Punkt \(Q\), auf der Kante \([BE]\) der Punkt \(R(0|6|2)\). Das Dreieck \(FQR\) hat in \(Q\) einen rechten Winkel. Bestimmen Sie die \(x_3\)-Koordinate von \(Q\).
(5 BE)
- Details
- Kategorie: Geometrie 2
Der Körper wird so um die Gerade \(AB\) gedreht, dass der mit \(D\) bezeichnete Eckpunkt nach der Drehung in der \(x_1x_2\)-Ebene liegt und dabei eine positive \(x_2\)-Koordinate hat. Die folgenden Rechnungen liefern die Lösung einer Aufgabe im Zusammenhang mit der Drehung:
\(\begin{pmatrix} 6 \\ -3 \\ 0 \end{pmatrix} \circ \left[ \begin{pmatrix} 0 \\ 6 \\ 0 \end{pmatrix} + \lambda \cdot \begin{pmatrix} 6 \\ -3 \\ 0 \end{pmatrix} - \begin{pmatrix} 3 \\ 0 \\ 0 \end{pmatrix} \right] = 0 \; \Leftrightarrow \; \lambda = 0{,}8\), d. h. \(S(4{,}8|3{,}6|0)\)
\(\overrightarrow{T} = \overrightarrow{S} + \vert \overrightarrow{CS} \vert \cdot \begin{pmatrix} 0 \\ 0 \\ 1 \end{pmatrix}\)
Formulieren Sie eine passende Aufgabenstellung und geben Sie die Bedeutung von \(S\) an.
(3 BE)

