Im Mittelpunkt des Grundstücks wird ein Mast errichtet, der durch vier an seiner Spitze befestigte Seile gehalten wird. Die Verankerungspunkte der Seile im Grundstücksboden sind jeweils 15 m vom Mastfußpunkt entfernt und liegen von diesem aus genau in östlicher, nördlicher, westlicher und südlicher Richtung.
Bestimmen Sie im Modell die Koordinaten des östlichen und nördlichen Verankerungspunkts \(V_O\) bzw. \(V_N\).
(5 BE)
Lösung zu Teilaufgabe f
Östlicher Verankerungspunkt \(V_O\)
Die positive \(x_2\)-Achse beschreibt die östliche Himmelsrichtung (siehe Teilaufgabe c).
\(\Longrightarrow \quad \begin {pmatrix} 0 \\ 1 \\ 0 \end {pmatrix}\) ist Einheitsvektor in östlicher Richtung.
\[\begin{align*} \overrightarrow {V}_O &= \overrightarrow M + 15 \cdot \begin {pmatrix} 0 \\ 1 \\ 0 \end {pmatrix} \\[0.8em] &= \begin {pmatrix} -40 \\ 30 \\ 30 \end {pmatrix} + 15 \cdot \begin {pmatrix} 0 \\ 1 \\ 0 \end {pmatrix} \\[0.8em] &= \begin {pmatrix} -40 \\ 45 \\ 30 \end {pmatrix} \end{align*}\]
\[\Longrightarrow \quad V_O(-40|45|30)\]
Nördlicher Verankerungspunkt \(V_N\)
Einheitsvektor in nördlicher Hangrichtung:
\[\frac{\overrightarrow{OC}}{\left| \overrightarrow{OC} \right|} = \frac{\overrightarrow C}{\left| \overrightarrow C \right|}; \qquad \overrightarrow C = \begin {pmatrix} -80 \\ 0 \\ 60 \end {pmatrix} = 20 \cdot \begin {pmatrix} -4 \\ 0 \\ 3 \end {pmatrix}\]
Betrag eines Vektors
\[ \vert \overrightarrow{a} \vert = \sqrt{\overrightarrow{a} \circ \overrightarrow{a}} = \sqrt{{a_1}^2 + {a_2}^2 + {a_3}^2}\]
(vgl. Merkhilfe)
\[\frac{\overrightarrow C}{\left| \overrightarrow C \right|} = \frac{\begin {pmatrix} -4 \\ 0 \\ 3 \end {pmatrix}}{\left| \begin {pmatrix} -4 \\ 0 \\ 3 \end {pmatrix} \right|} = \frac{\begin {pmatrix} -4 \\ 0 \\ 3 \end {pmatrix}}{\sqrt{(-4)^2 + 0^2 + 3^2}} = \frac{1}{5} \cdot \begin {pmatrix} -4 \\ 0 \\ 3 \end {pmatrix}\]
\[\begin{align*} \overrightarrow {V}_N &= \overrightarrow M + 15 \cdot \frac{\overrightarrow C}{\left| \overrightarrow C \right|} \\[0.8em] &= \begin {pmatrix} -40 \\ 30 \\ 30 \end {pmatrix} + 15 \cdot \frac{1}{5} \cdot \begin {pmatrix} -4 \\ 0 \\ 3 \end {pmatrix} \\[0.8em] &= \begin {pmatrix} -52 \\ 30 \\ 39 \end {pmatrix} \end{align*}\]
\[\Longrightarrow \quad V_N(-52|30|39)\]
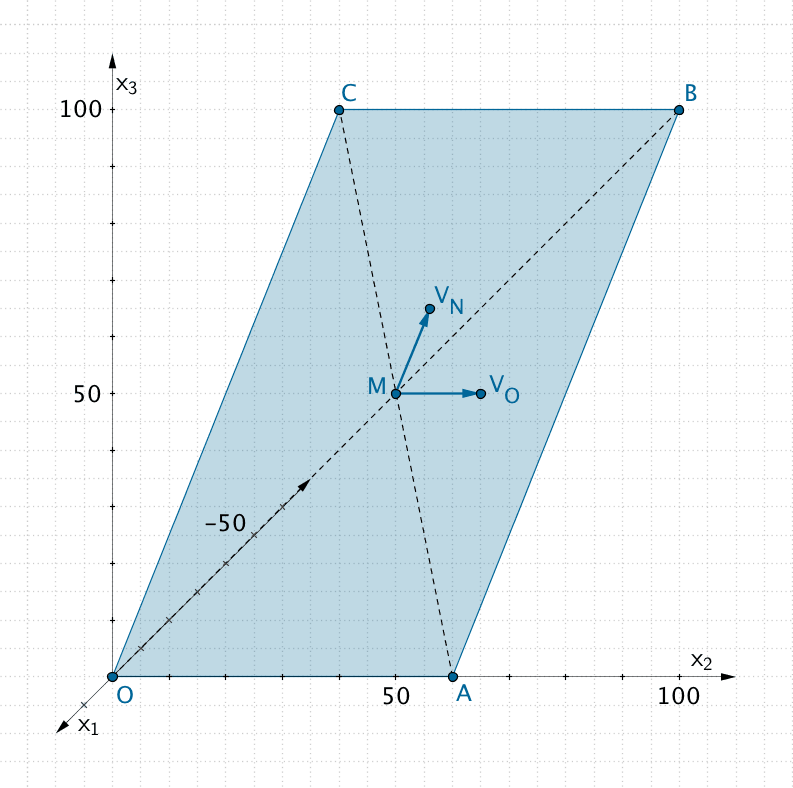
Lage des östlichen Verankerungspunktes \(V_O\) und des nördlichen Verankerungspunktes \(V_N\)

