Die drei leeren Seiten des Würfels sollen jeweils mit einer positiven geraden Zahl beschriftet werden. Ermitteln Sie eine Möglichkeit für die Beschriftung dieser drei Seiten, sodass bei einmaligem Werfen des Würfels der Erwartungswert für die Zahl \(\dfrac{31}{6}\) beträgt.
(3 BE)
Lösung zu Teilaufgabe b
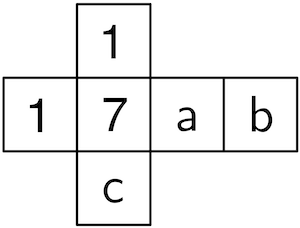
Beispielsweise wählt man \(a\), \(b\) und \(c\) stellvertretend für die Beschriftung der drei leeren Seiten des Würfels mit positiven geraden Zahlen.
Es sei \(X\) die Zufallsgröße, welche die erzielte Zahl bei einmaligem Werfen des Würfels beschreibt.
Es ergibt sich folgende Wahrscheinlichkeitsverteilung von \(X\):
| \(\textcolor{#cc071e}{X = x_i}\) | \(\textcolor{#cc071e}{1}\) | \(\textcolor{#cc071e}{7}\) | \(\textcolor{#cc071e}{a}\) | \(\textcolor{#cc071e}{b}\) | \(\textcolor{#cc071e}{c}\) |
| \(\textcolor{#0087c1}{P(X = x_i)}\) | \(\textcolor{#0087c1}{\dfrac{1}{3}}\) | \(\textcolor{#0087c1}{\dfrac{1}{6}}\) | \(\textcolor{#0087c1}{\dfrac{1}{6}}\) | \(\textcolor{#0087c1}{\dfrac{1}{6}}\) | \(\textcolor{#0087c1}{\dfrac{1}{6}}\) |
Bei einmaligem Werfen des Würfels soll der Erwartungswert für die erzielte Zahl \(\dfrac{31}{6}\) betragen (vgl. Angabe).
Ist \(X\) eine Zufallsgröße, deren mögliche Werte \(x_{1}, x_{2}, ..., x_{n}\) sind, dann gilt:
Erwartungswert \(\boldsymbol{\mu}\) der Zufallsgröße \(\boldsymbol{X}\) (vgl. Merkhilfe)
\[\begin{align*}\mu = E(X) &= \sum \limits_{i = 1}^{n} x_{i} \cdot p_{i} \\[0.8em] &= x_{1} \cdot p_{1} + x_{2} \cdot p_{2} \,+\, ... \,+\, x_{n} \cdot p_{n} \end{align*}\]
Der Erwartungswert \(\boldsymbol{\mu}\) einer Zufallsgröße \(X\) gibt den Mittelwert der Zufallsgröße an, der bei oftmaliger Wiederholung eines Zufallsexperiments zu erwarten ist.
\[\begin{align*} E(X) & = \frac{31}{6} \\[0.8em]\textcolor{#cc071e}{1} \cdot \textcolor{#0087c1}{\dfrac{1}{3}} + \textcolor{#cc071e}{7} \cdot \textcolor{#0087c1}{\dfrac{1}{6}} + \textcolor{#cc071e}{a} \cdot \textcolor{#0087c1}{\dfrac{1}{6}} + \textcolor{#cc071e}{b} \cdot \textcolor{#0087c1}{\dfrac{1}{6}} + \textcolor{#cc071e}{c} \cdot \textcolor{#0087c1}{\dfrac{1}{6}} &= \frac{31}{6} &&| \cdot 6 \\[0.8em] 2 + 7 + a + b + c &= 31 \\[0.8em] 9 + a + b + c &= 31 &&| - 9 \\[0.8em] a + b + c &= 22 \end{align*}\]
Mögliche Beschriftungen der drei leeren Seiten sind somit:
\(a = 4\); \(b = 8\); \(c = 10\)
\(a = 6\); \(b = 8\); \(c = 8\)
\(a = 10\); \(b = 10\); \(c = 2\)
usw.


