Die Schnittfigur von \(k_{1}\) und \(k_{2}\) ist ein Kreis. Bestimmen Sie die Koordinaten des Mittelpunkts und den Radius dieses Kreises.
(3 BE)
Lösung zu Teilaufgabe 1b
\[k_{1} \colon M_{1}(1|2|3); \; r_{1} = 5\]
\[k_{2} \colon M_{2}(-3|-2|1); \; r_{2} = 5\]
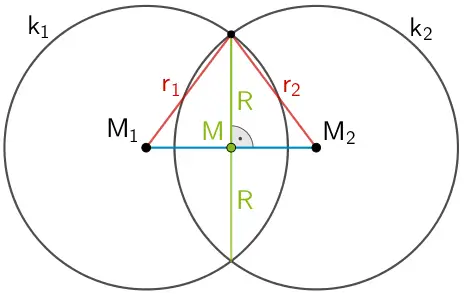
Schnittkreis der Kugeln \(k_{1}\) und \(k_{2}\) mit Mittelpunkt \(\textcolor{#89ba17}{M}\) und Radius \(\textcolor{#89ba17}{R}\)
Koordinaten des Mittelpunkts des Schnittkreises
Da die Kugeln \(k_{1}\) und \(k_{2}\) den Radius \(\textcolor{#cc071e}{r_{1} = r_{2} = 5}\) besitzen, ist der Mittelpunkt \(\textcolor{#89ba17}{M}\) des Schnittkreises der Mittelpunkt der Strecke \([M_{1}M_{2}]\).
Mittelpunkt einer Strecke
Für den Ortsvektor \(\overrightarrow{M}\) des Mittelpunkts \(M\) einer Strecke \([AB]\) gilt:
\[\overrightarrow{M} = \frac{1}{2} \left( \overrightarrow{A} + \overrightarrow{B} \right)\]
\[\begin{align*} \overrightarrow{M} &= \frac{1}{2} \cdot (\overrightarrow{M_{1}} + \overrightarrow{M_{2}}) \\[0.8em] &= \frac{1}{2} \cdot \left[ \begin{pmatrix} 1 \\ 2 \\ 3 \end{pmatrix} + \begin{pmatrix} -3 \\ -2 \\ 1 \end{pmatrix} \right] \\[0.8em] &= \frac{1}{2} \cdot \begin{pmatrix} -2 \\ 0 \\ 4 \end{pmatrix} \\[0.8em] &= \begin{pmatrix} -1 \\ 0 \\ 2 \end{pmatrix} \end{align*}\]
\[\Longrightarrow \quad M(-1|0|2)\]
Radius des Schnittkreises
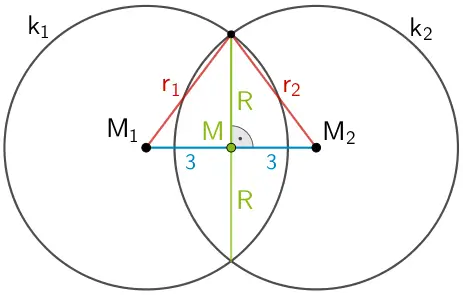
Mithilfe des Satzes des Pythagoras ergibt sich:
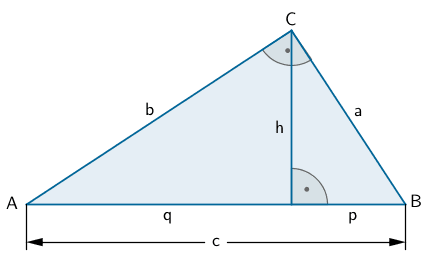
Satzgruppe des Pythagoras im rechtwinkligen Dreieck
Satz des Pythagoras
\[\hspace{5px}a^2 + b^2 = c^2\]
Höhensatz
\[h^2 = p \cdot q\]
Kathetensatz
\[a^2 = c \cdot p\,; \enspace b^2 = c \cdot q\]
\[\begin{align*} \textcolor{#0087c1}{\overline{M_{1}M}}^{2} + \textcolor{#89ba17}{R}^{2} &= \textcolor{#cc071e}{r_{1}}^{2} &&| \; -\overline{M_{1}M} \\[0.8em] R^{2} &= {r_{1}}^{2} - \overline{M_{1}M}^{2} \\[0.8em] R &= \sqrt{{r_{1}}^{2} - \overline{M_{1}M}^{2}} \\[0.8em] \textcolor{#89ba17}{R} &= \sqrt{\textcolor{#cc071e}{5}^{2} - \textcolor{#00871e}{3}^{2}} \\[0.8em] &= \sqrt{16} \\[0.8em] &= 4 \end{align*}\]


