- Details
- Kategorie: Analysis 2
Gegeben ist die Funktion \(f\) mit \(f(x) = \sqrt{x - 2} + 1\) und maximalem Definitionsbereich.
Zeichnen Sie den Graphen von \(f\) im Bereich \(2 \leq x \leq 11\) in ein Koordinatensystem.
(3 BE)
- Details
- Kategorie: Analysis 2
Berechnen Sie den Wert des Integrals \(\displaystyle \int_{2}^{3} f(x)dx\).
(3 BE)
- Details
- Kategorie: Analysis 2
Geben Sie jeweils den Term einer in \(\mathbb R\) definierten Funktion an, die die angegebene Wertemenge \(W\) hat.
\[W =\; ]-\infty;1]\]
(2 BE)
- Details
- Kategorie: Analysis 2
Geben Sie jeweils den Term einer in \(\mathbb R\) definierten Funktion an, die die angegebene Wertemenge \(W\) hat.
\[W =\; ]3;+\infty[\]
(2 BE)
- Details
- Kategorie: Analysis 2
Betrachtet werden eine in \(\mathbb R\) definierte ganzrationale Funktion \(p\) und der Punkt \(Q(2|p(2))\).
Beschreiben Sie, wie man rechnerisch die Gleichung der Tangente an den Graphen von \(p\) im Punkt \(Q\) ermitteln kann.
(2 BE)
- Details
- Kategorie: Analysis 2
Gegeben ist eine in \(\mathbb R\) definierte Funktion \(h \colon x \mapsto ax^{2} + c\) mit \(a, c \in \mathbb R\), deren Graph im Punkt \(N(1|0)\) die Tangente mit der Gleichung \(y = -x + 1\) besitzt. Bestimmen Sie \(a\) und \(c\).
(3 BE)
- Details
- Kategorie: Analysis 2
Die Abbildung zeigt den Graphen \(G_{f}\) einer in \(\mathbb R\) definierten Funktion \(f\). \(G_{f}\) ist streng monoton fallend und schneidet die \(x\)-Achse im Punkt \((1|0)\).
Betrachtet wird ferner die Funktion \(g\) mit \(g(x) = \dfrac{1}{f(x)}\) und maximalem Definitionsbereich \(D_{g}\).
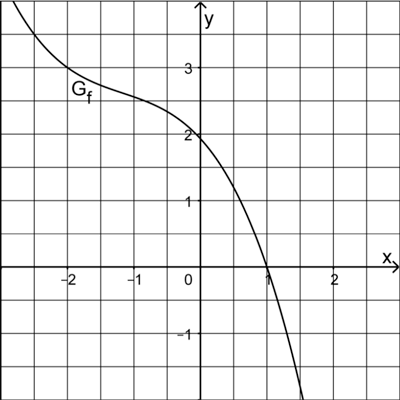
Begründen Sie, dass \(x = 1\) nicht in \(D_{g}\) enthalten ist, und geben Sie den Funktionswert \(g(-2)\) an.
(2 BE)
- Details
- Kategorie: Analysis 2
Ermitteln Sie mithilfe der Abbildung die \(x\)-Koordinaten der Schnittpunkte der Graphen von \(f\) und \(g\).
(3 BE)

