Geben Sie für die Funktion \(h\) und deren Ableitungsfunktion \(h'\) jeweils das Verhalten für \(x \to 0\) an und zeichnen Sie \(G_{h}\) im Bereich \(0 < x < 0{,}75\) in Abbildung 1 ein.
(3 BE)
Lösung zu Teilaufgabe 1c
Grenzwertbetrachtung, Funktionsgraph zeichnen
Anmerkung:
Das Verhalten der Funktion \(h\) und deren Ableitungsfunktion \(h'\) für \(x \to 0\) ist jeweils lediglich anzugeben. Jede Erklärung kann entfallen.
Verhalten der Funktion \(h\) für \(x \to 0\)
\[h(x) = 3x \cdot (-1 + \ln{x}); \; D_{h} = \mathbb R^{+}\]
Das Verhalten der Funktion \(h\) für \(x \to 0\) lässt sich mithilfe des in der Merkhilfe dokumentierten Grenzwerts \(\lim \limits_{x\,\to\,0} \left( x^{r} \cdot \ln{x} \right) = 0 \; (r > 0) \) angeben.
Wichtiger Grenzwert
\[\lim \limits_{x \, \to \, 0} \left( x^{r} \cdot \ln{x} \right) = 0 \enspace (r > 0)\]
(vgl. Merkhilfe)
\[\lim \limits_{x\,\to\,0} h(x) = \lim \limits_{x\,\to\,0} 3x \cdot (-1 + \ln{x}) = 0\]
Für \(x \to 0\) nähert sich der Graph der Funktion \(h\) beliebig nahe dem Koordinatenursprung \(O(0|0)\).
Alternative: Regel von L'Hospital anwenden
Regel von L'Hospital
Führt der Grenzwert \(\,\displaystyle \lim \limits_{x\,\to\,x_0} \frac{f(x)}{g(x)}\,\) auf den unbestimmten Ausdruck \(\displaystyle \,\frac{0}{0}\,\) oder \(\displaystyle \,\frac{\infty}{\infty}\,\),
und existiert der Grenzwert \(\displaystyle \,\lim \limits_{x\,\to\,x_0} \frac{f'(x)}{g'(x)}\,\), so gilt:
\[\lim \limits_{x\,\to\,x_0} \frac{f(x)}{g(x)} = \lim \limits_{x\,\to\,x_0} \frac{f'(x)}{g'(x)}\]
Die Regel kann anstelle \(\,x \to x_0\,\) auch für \(\,x \to \infty\,\) oder \(\,x \to -\infty\,\) angewendet werden.
Anmerkung:
Die Regel von L'Hospital ist nicht im G8 Mathematik Lehrplan enthalten. Erfahrungsgemäß wird diese aber des Öfteren optional unterrichtet, um Grenzwertbetrachtungen von unbestimmten Ausdrücken der Form \(\dfrac{0}{0}\) oder \(\dfrac{\infty}{\infty}\) zu vertiefen.
\[h(x) = 3x \cdot (-1 + \ln{x}); \; D_{h} = \mathbb R^{+}\]
Ableitung der natürlichen Logarithmusfunktion
\[f(x) = \ln x \enspace (x > 0) \quad \Longrightarrow \quad f'(x) = \frac{1}{x}\]
Ableitung einer Potenzfunktion
\[f(x) = x^r \quad \Longrightarrow \quad f'(x) = rx^{r - 1} \quad (r \in \mathbb R)\]
Faktorregel
\(f(x) = a \cdot u(x) \quad \Longrightarrow \quad f'(x) = a \cdot u'(x)\)
Summenregel
\(f(x) = u(x) + v(x) \quad \Longrightarrow \quad f'(x) = u'(x) + v'(x)\)
(vgl. Merkhilfe)
\[\begin{align*} \lim \limits_{x\,\to\,0} h(x) &= \lim \limits_{x\,\to\,0} \underbrace{\underbrace{3x}_{\to\,0} \cdot \underbrace{(-1 + \ln{x})}_{\to\,-\infty}}_{\large{0\,\cdot\,-\infty}} & &| \; \text{Umschreiben in die Form} \; \dfrac{\infty}{\infty} \\[0.8em] &= \lim \limits_{x\,\to\,0} \underbrace{\frac{3 \cdot (-1 + \ln{x})}{\frac{1}{x}}}_{\large{-\frac{\infty}{\infty}}} \\[0.8em] &= \lim \limits_{x\,\to\,0} \frac{ \left[3 \cdot (-1 +\ln{x})\right]'}{\left( \frac{1}{x} \right)'} & &| \; \left[3 \cdot (-1 +\ln{x})\right]' = \frac{3}{x}; \; \left( \frac{1}{x} \right)' = -\frac{1}{x^{2}} \\[0.8em] &= \lim \limits_{x\,\to\,0} \frac{\frac{3}{x}}{-\frac{1}{x^{2}}} \\[0.8em] &= \lim \limits_{x\,\to\,0} -\frac{3x^{2}}{x} & &| \; (x \neq 0) \\[0.8em] &= \lim \limits_{x\,\to\,0} -3x \\[0.8em] &= 0 \end{align*}\]
Verhalten der Ableitungsfunktion \(h'\) für \(x \to 0\)
\(h'(x) = 3 \cdot \ln{x}\) (vgl. Teilaufgabe 1a)
\[\lim \limits_{x\,\to\,0} h'(x) = \lim \limits_{x\,\to\,0} 3 \cdot \underbrace{\ln{x}}_{\to\,-\infty} = -\infty\]
Geometrische Interpretation des Grenzwerts:
Die Ableitung \(h'\) beschreibt die Steigung einer Tangente an den Graphen der Funktion \(h\). Für \(x \to 0\) nähert sich die Steigung der Tangente dem Grenzwert \(-\infty\), was einer nahezu senkrecht zur \(x\)-Achse verlaufenden Tangente entspricht. Das bedeutet, dass der Graph der Funktion \(h\) in der Umgebung des Koordinatenursprungs \(O(0|0)\) senkrecht zur \(x\)-Achse mündet. Die nachfolgende Zeichnung sollte dieses Verhalten von \(G_{h}\) erkennen lassen.
Zeichnung von \(G_{h}\) im Bereich \(0 < x < 0{,}75\)
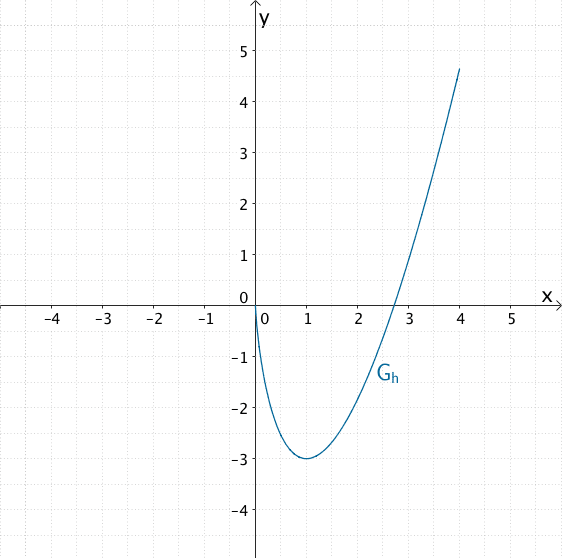
Graph \(G_{h}\) der in \(\mathbb R^{+}\) definierten Funktion \(h \colon x \mapsto 3x \cdot (-1 + \ln{x})\) für \(0 < x \leq 4\)


