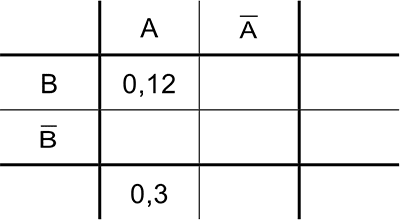
Nebenstehende Vierfeldertafel gehört zu einem Zufallsexperiment mit den stochastisch unabhängigen Ereignissen \(A\) und \(B\). Tragen Sie alle fehlenden Wahrscheinlichkeiten ein.
(3 BE)
Lösung zu Teilaufgabe 1a
Vierfeldertafel, Stochastische Unabhängigkeit zweier Ereignisse
Die Summe der Wahrscheinlichkeiten der Ereignisse bzw. Teilmengen, die den Ergebnisraum \(\Omega\) abbilden, ist gleich Eins.
\[P(A) + P(\overline{A}) = P(\Omega) = 1\]
bzw.
\[P(B) + P(\overline{B}) = P(\Omega) = 1\]
bzw.
\[P(A \cap B) + P(A \cap \overline{B}) + P(\overline{A} \cap B) + P(\overline{A} \cap \overline{B}) = P(\Omega) = 1\]
| \(A\) | \(\overline{A}\) | ||
| \(B\) | \(0{,}12\) | \(\qquad\) | |
| \(\overline{B}\) | |||
| \(0{,}3\) | \(\boldsymbol{P(\Omega) = 1}\) |
Die weitere Vorgehensweise kann in der Reihenfolge variieren.
Die Wahrscheinlichkeit der Schnittmenge \(A \cap B\) und des Ereignisses \(\overline{A}\) lässt sich spalten- bzw- zeilenweise durch Subtraktion ermitteln.
\[P(A \cap \overline{B}) = P(A) - P(A \cap B) = 0{,}3 - 0{,}12 = 0{,}18\]
\[P(\overline{A}) = P(\Omega) - P(A) = 1 - 0{,}3 = 0{,}7\]
| \(A\) | \(\overline{A}\) | ||
| \(B\) | \(0{,}12\) | ||
| \(\overline{B}\) | \(\boldsymbol{0{,}18}\) | ||
| \(0{,}3\) | \(\boldsymbol{0{,}7}\) | \(1\) |
Um die Vierfeldertafel vollständig ausfüllen zu können, wird die Wahrscheinlichkeit des Ereignisses \(B\) oder \(\overline{B}\) benötigt.
Die Ereignisse \(A\) und \(B\) sind stochastisch unabhängig (vgl. Angabe).
Folglich gilt:
Stochastische (Un)Abhängigkeit von zwei Ereignissen
Zwei Ereignisse \(A\) und \(B\) heißen stochastisch unabhängig, wenn
\(P(A) \cdot P(B) = P(A \cap B)\) gilt. (vgl. Merkhilfe) *
Andernfalls heißen die Ereignisse \(A\) und \(B\) stochastisch abhängig.
Sind zwei Ereignisse \(A\) und \(B\) stochastisch unabhängig, beeinflusst das Eintreten des Ereignisses \(A\) nicht das Eintreten des Ereignisses \(B\) und umgekehrt.
* Oder wenn
\(P(\overline{A}) \cdot P(B) = P(\overline{A} \cap B)\) bzw.
\(P(A) \cdot P(\overline{B}) = P(A \cap \overline{B})\) bzw.
\(P(\overline{A}) \cdot P(\overline{B}) = P(\overline{A} \cap \overline{B})\) gilt.
\[P(A \cap B) = P(A) \cdot P(B)\]
bzw.
\[P(A \cap \overline{B}) = P(A) \cdot P(\overline{B})\]
Anmerkung:
Im Falle zweier stochastisch unabhängiger Ereignisse \(A\) und \(B\) gilt:
\(P(A \cap B) = P(A) \cdot P(B)\) und
\(P(\overline{A} \cap B) = P(\overline{A}) \cdot P(B)\) und
\(P(A \cap \overline{B}) = P(A) \cdot P(\overline{B})\) und
\(P(\overline{A} \cap \overline{B}) = P(\overline{A}) \cdot P(\overline{B})\).
Damit lässt sich die Wahrscheinlichkeit \(P(B)\) oder \(P(\overline{B})\) berechnen:
\[\begin{align*} P(A \cap B) &= P(A) \cdot P(B) \\[0.8em] \Longleftrightarrow \enspace P(B) &= \frac{P(A \cap B)}{P(A)} \\[0.8em] &= \frac{0{,}12}{0{,}3} \\[0.8em] &= 0{,}4 \end{align*}\]
| \(A\) | \(\overline{A}\) | ||
| \(B\) | \(0{,}12\) | \(\boldsymbol{0{,}4}\) | |
| \(\overline{B}\) | \(0{,}18\) | ||
| \(0{,}3\) | \(0{,}7\) | \(1\) |
oder
\[\begin{align*} P(A \cap \overline{B}) &= P(A) \cdot P(\overline{B}) \\[0.8em] \Longleftrightarrow \enspace P(\overline{B}) &= \frac{P(A \cap \overline{B})}{P(A)} \\[0.8em] &= \frac{0{,}18}{0{,}3} \\[0.8em] &= 0{,}6 \end{align*}\]
| \(A\) | \(\overline{A}\) | ||
| \(B\) | \(0{,}12\) | ||
| \(\overline{B}\) | \(0{,}18\) | \(\boldsymbol{0{,}6}\) | |
| \(0{,}3\) | \(0{,}7\) | \(1\) |
Abschließend kann die Vierfeldertafel spalten- bzw. zeilenweise durch Subtraktion vervollständigt werden, beispielsweise wie folgt:
\[P(\overline{B}) = P(\Omega) - P(B) = 1 - 0{,}4 = 0{,}6\]
\[P(\overline{A} \cap B) = P(B) - P(A \cap B) = 0{,}4 - 0{,}12 = 0{,}28\]
\[P(\overline{A} \cap \overline{B}) = P(\overline{B}) - P(A \cap \overline{B}) = 0{,}6 - 0{,}18 = 0{,}42\]
| \(A\) | \(\overline{A}\) | ||
| \(B\) | \(0{,}12\) | \(\boldsymbol{0{,}28}\) | \(0{,}4\) |
| \(\overline{B}\) | \(0{,}18\) | \(\boldsymbol{0{,}42}\) | \(\boldsymbol{0{,}6}\) |
| \(0{,}3\) | \(0{,}7\) | \(1\) |
oder
\[P(B) = P(\Omega) - P(\overline{B}) = 1 - 0{,}6 = 0{,}4\]
\[P(\overline{A} \cap B) = P(B) - P(A \cap B) = 0{,}4 - 0{,}12 = 0{,}28\]
\[P(\overline{A} \cap \overline{B}) = P(\overline{B}) - P(A \cap \overline{B}) = 0{,}6 - 0{,}18 = 0{,}42\]
| \(A\) | \(\overline{A}\) | ||
| \(B\) | \(0{,}12\) | \(\boldsymbol{0{,}28}\) | \(\boldsymbol{0{,}4}\) |
| \(\overline{B}\) | \(0{,}18\) | \(\boldsymbol{0{,}42}\) | \(0{,}6\) |
| \(0{,}3\) | \(0{,}7\) | \(1\) |
Anmerkung:
Im Falle zweier stochastisch unabhängiger Ereignisse \(A\) und \(B\) ist die Vierfeldertafel der Wahrscheinlichkeiten eine Multiplikationstafel. Das bedeutet, dass die Einträge der inneren Zellen das Produkt der Einträge der zugehörigen Randzellen sind.
| \(A\) | \(\overline{A}\) | ||
| \(B\) | \(P(A \cap B) = P(A) \cdot P(B)\) | \(P(\overline{A} \cap B) = P(\overline{A}) \cdot P(B)\) | \(P(B)\) |
| \(\overline{B}\) | \(P(A \cap \overline{B}) = P(A) \cdot P(\overline{B})\) | \(P(\overline{A} \cap \overline{B}) = P(\overline{A}) \cdot P(\overline{B})\) | \(P(\overline{B})\) |
| \(P(A)\) | \(P(\overline{A})\) | \(1\) |
Vierfeldertafel der Wahrscheinlichkeiten zweier stochastisch unabhängiger Ereignisse \(A\) und \(B\)


