Gegeben ist ein Rechteck \(ABCD\) mit den Eckpunkten \(A(5|-4|-3)\), \(B(5|4|3)\), \(C(0|4|3)\) und \(D\).

Ermitteln Sie die Koordinaten von \(D\) und geben Sie die Koordinaten des Mittelpunkts \(M\) der Strecke \([AC]\) an.

(3 BE)

Lösung zu Teilaufgabe 1a

Koordinaten des Punktes \(D\)

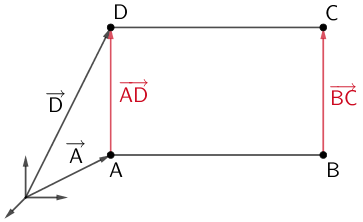
Die Koordinaten des Punktes \(D\) lassen sich durch Vektorasddition bestimmen, beispielsweise wie folgt (Zeichnung schematisch):

\(A(5|-4|-3)\), \(B(5|4|3)\), \(C(0|4|3)\)

\[\begin{align*} \overrightarrow{D} &= \overrightarrow{A} + \textcolor{#cc071e}{\overrightarrow{AD}} &&| \; \textcolor{#cc071e}{\overrightarrow{AD} = \overrightarrow{BC}} \\[0.8em] &= \overrightarrow{A} + \overrightarrow{BC} \\[0.8em] &= \overrightarrow{A} + (\overrightarrow{C} - \overrightarrow{B}) \\[0.8em] &= \begin{pmatrix} 5 \\ -4 \\ -3 \end{pmatrix} + \left[ \begin{pmatrix} 0 \\ 4 \\ 3 \end{pmatrix} - \begin{pmatrix} 5 \\ 4 \\ 3 \end{pmatrix} \right] \\[0.8em] &= \begin{pmatrix} 5 \\ -4 \\ -3 \end{pmatrix} + \begin{pmatrix} -5 \\ 0 \\ 0 \end{pmatrix} \\[0.8em] &= \begin{pmatrix} 0 \\ -4 \\ -3 \end{pmatrix} \end{align*}\]

\[\Longrightarrow \quad D(0|-4|-3)\]

Koordinaten des Mittelpunkts \(M\) der Strecke \([AC]\)

\(A(5|-4|-3)\), \(C(0|4|3)\)

\[\begin{align*}\overrightarrow{M} &= \frac{1}{2} \cdot (\overrightarrow{A} + \overrightarrow{C}) \\[0.8em] &= \frac{1}{2} \cdot \left[ \begin{pmatrix} 5 \\ -4 \\ -3 \end{pmatrix} + \begin{pmatrix} 0 \\ 4 \\ 3 \end{pmatrix} \right] \\[0.8em] &= \frac{1}{2} \cdot \begin{pmatrix} 5 \\ 0 \\ 0 \end{pmatrix} \\[0.8em] &= \begin{pmatrix} 2{,}5 \\ 0 \\ 0 \end{pmatrix} \end{align*}\]

\[\Longrightarrow \quad M(2{,}5|0|0)\]