Gegeben ist die in \(\mathbb R\) definierte Funktion \(f\) mit \(f(x) = x \cdot e^{-\frac{1}{2}x^2+\frac{1}{2}}\). Die Abbildung 1 zeigt den Graphen von \(f\) ohne das zugrunde liegende Koordinatensystem.
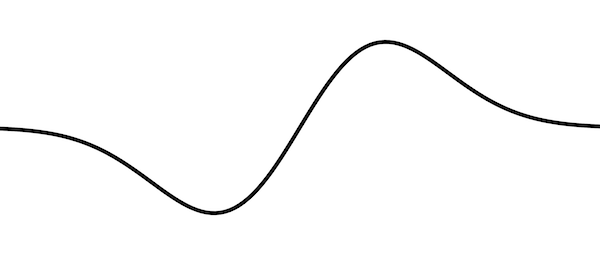Abb. 1
Zeigen Sie anhand des Funktionsterms von \(f\), dass der Graph von \(f\) symmetrisch bezüglich des Koordinatenursprungs ist. Begründen Sie, dass \(f\) genau eine Nullstelle hat, und geben Sie den Grenzwert von \(f\) für \(x \to +\infty\) an.
(4 BE)
Lösung zu Teilaufgabe 1a
Nachweis, dass der Graph von \(f\) symmetrisch bezüglich des Koordinatenursprungs ist
\[f(x) = x \cdot e^{-\frac{1}{2}x^2+\frac{1}{2}}; \; D_f = \mathbb R\]
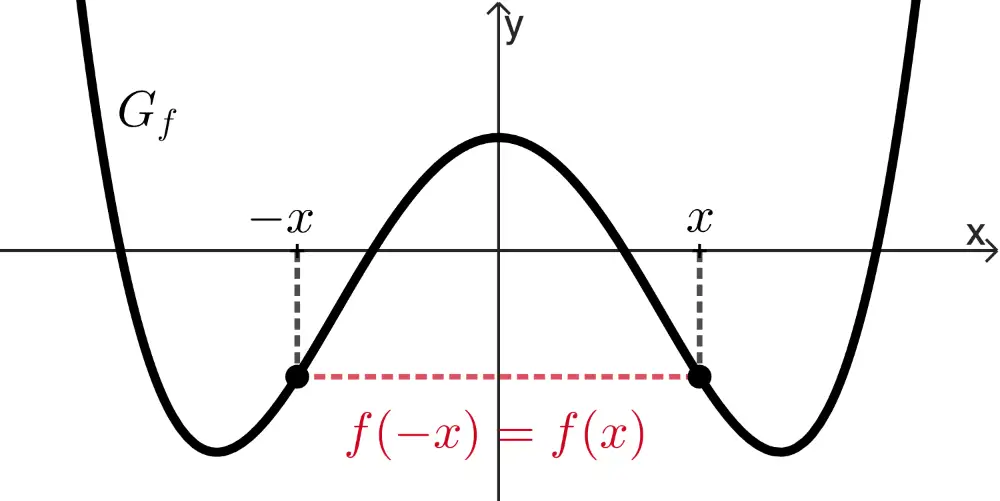
Symmetrie von Funktionsgraphen bzgl. des Koordinatensystems
Der Graph einer Funktion \(f\) ist
achsensymmetrisch bzgl. der \(\boldsymbol{y}\)-Achse,
wenn für alle \(x \in D_f\) gilt: \(f(-x) = f(x)\).
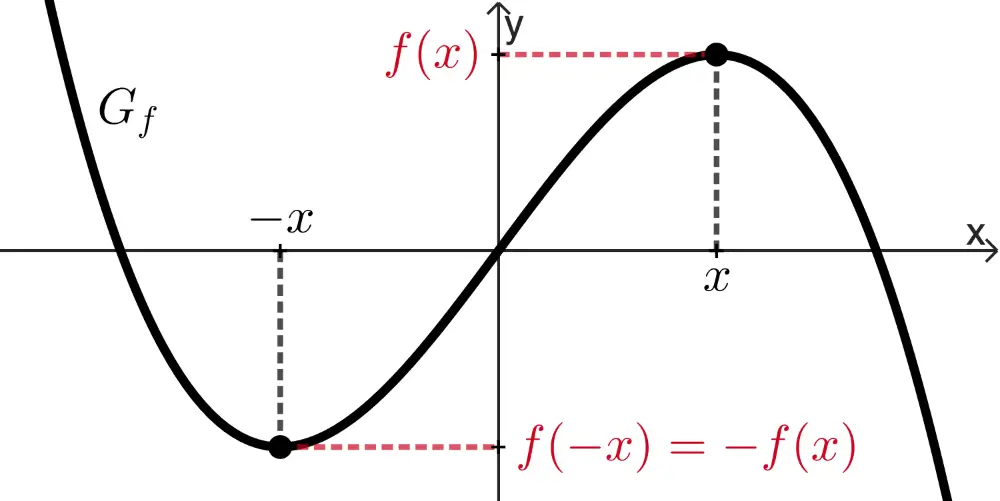
punktsymmetrisch bzgl. des Koordinatenursprungs,
wenn für alle \(x \in D_f\) gilt: \(f(-x) = -f(x)\)
\[f(\textcolor{#cc071e}{-x}) = \textcolor{#cc071e}{-x} \cdot e^{-\frac{1}{2} \cdot \textcolor{#cc071e}{(-x)}^2+\frac{1}{2}} = -x \cdot e^{-\frac{1}{2}x^2+\frac{1}{2}} = \textcolor{#cc071e}{-}f(x)\]
Da \(f(-x) = -f(x)\) gilt, ist der Graph der Funktion \(f\) symmetrisch bezüglich des Koordinatenursprungs.
Begründung, dass \(f\) genau eine Nullstelle hat
\[f(x) = \textcolor{#0087c1}{x} \cdot \textcolor{#e9b509}{\underbrace{e^{-\frac{1}{2}x^2+\frac{1}{2}}}_{>\,0}}; \; D_f = \mathbb R\]
Nullstelle(n) einer Funktion bestimmen
Eine Nullstelle ist die \(x\)-Koordinate eines gemeinsamen Punktes des Graphen einer Funktion \(x \mapsto f(x)\) mit der \(x\)-Achse. An einer Nullstelle gilt: \(f(x) = 0\).
Satz vom Nullprodukt: Ein Produkt ist genau dann null, wenn einer der Faktoren null ist.
\(f(x) \cdot g(x) = 0 \enspace \Rightarrow \enspace f(x) = 0\) oder \(g(x) = 0\)
Ein Quotient von Funktionen ist genau dann null, wenn die Zählerfunktion null ist.
\(\dfrac{f(x)}{g(x)} = 0 \enspace \Rightarrow \enspace f(x) = 0\; (g(x) \neq 0)\)
Lösungsformel für quadratische Gleichungen (Mitternachtsformel, vgl. Merkhilfe)
\[\textcolor{#cc071e}{a}x^2 + \textcolor{#0087c1}{b}x + \textcolor{#e9b509}{c} = 0 \enspace \Leftrightarrow \enspace x_{1,2} = \frac{-\textcolor{#0087c1}{b} \pm \sqrt{\textcolor{#0087c1}{b}^2 - 4\textcolor{#cc071e}{a}\textcolor{#e9b509}{c}}}{2\textcolor{#cc071e}{a}}\]
Diskriminante \(D = b^2 -4ac \;\):
\(D < 0\,\): keine Lösung
\(D = 0\,\): genau eine Lösung
\(D > 0\,\): zwei verschiedene Lösungen
Folgende Fälle lassen sich einfacher durch Umformung lösen:
\[\begin{align*}\textcolor{#cc071e}{a}x^2 + \textcolor{#0087c1}{b}x &= 0 &&| \; x\; \text{ausklammern (Produkt formulieren)} \\[0.8em] x \cdot (ax + b) &= 0 \\[0.8em] \Rightarrow \enspace x = 0 \vee ax + b &= 0 \end{align*}\]
\[\begin{align*}\textcolor{#cc071e}{a}x^2 + \textcolor{#e9b509}{c} &= 0 &&| -c \enspace (c \neq 0) \\[0.8em] ax^2 &= -c &&| : a \\[0.8em] x^2 &= -\frac{c}{a} &&| \; \sqrt{\quad} \\[0.8em] x_{1,2} &= \pm \sqrt{-\frac{c}{a}} \end{align*}\]
Zwei Lösungen, falls \(-\dfrac{c}{a} > 0\), keine Lösung, falls \(-\dfrac{c}{a} < 0\)
Vorgehensweise für die Bestimmung der Nullstelle(n) einer ganzrationalen Funktion ab Grad 3:
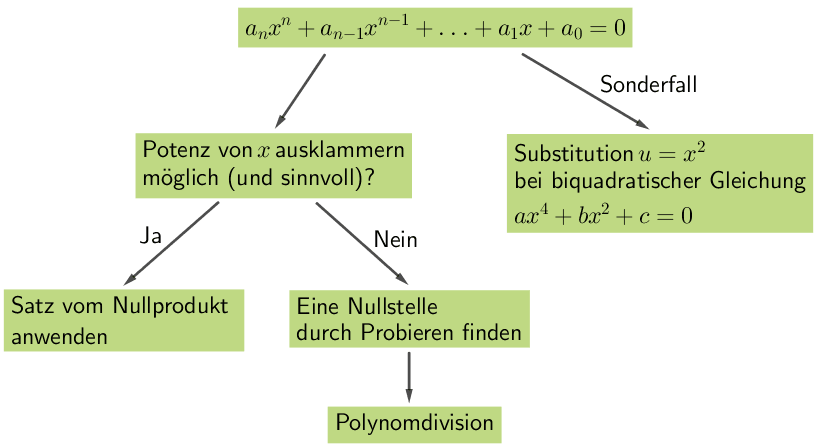
vgl. Abiturskript - 1.1.3 Ganzrationale Funktion, Nullstellen
Nullstellen einer gebrochenrationalen Funktion \(f(x) = \dfrac{\textcolor{#0087c1}{z(x)}}{n(x)}\) sind alle Nullstellen des Zählerpolynoms \(\textcolor{#0087c1}{z(x)}\), die nicht zugleich Nullstellen des Nennerpolynoms \(\boldsymbol{n(x)}\) sind.
Ist \(x_0\) eine Nullstelle des Zählerpolynoms \(\boldsymbol{z(x)}\) und zugleich eine vollständig kürzbare Nullstelle des Nennerpolynoms \(\boldsymbol{n(x)}\), so besitzt die gebrochenrationale Funktion \(f\) an der Stelle \(x_0\) eine hebbare Definitionslücke.
(vgl. Abiturskript - 1.2.1 Gebrochenrationale Funktion, Nullstellen und Polstellen)
Eine Wurzelfunktion \(f(x) = \sqrt{\textcolor{#cc071e}{g(x)}}\) nimmt genau dann den Wert null an, wenn der Radikand (Term unter der Wurzel) null ist.
\[\sin{x} = 0 \enspace \Rightarrow \enspace x = k \cdot \pi \; (k \in \mathbb Z)\]
\[\cos{x} = 0 \enspace \Rightarrow \enspace x = \dfrac{\pi}{2} + k \cdot \pi \; (k \in \mathbb Z)\]
Die natürliche Logarithmusfunktion \(x \mapsto \ln{x}\) besitzt die einzige Nullstelle \(\boldsymbol{x = 1}\).
\[\ln{\left( \textcolor{#0087c1}{f(x)} \right)} = 0 \enspace \Rightarrow \enspace \textcolor{#0087c1}{f(x) = 1}\]
Die natürliche Exponentialfunktion \(x \mapsto e^x\) sowie jede verkettete Funktion \(x \mapsto e^{f(x)}\) besitzt keine Nullstelle!
\[f(x) = 0 \enspace \Rightarrow \enspace \textcolor{#0087c1}{x = 0}\]
Da der Exponentialterm \(\textcolor{#e9b509}{e^{-\frac{1}{2}x^2+\frac{1}{2}}}\) für alle \(x \in \mathbb R\) stets positiv ist, ist \(x = 0\) die einzige Nullstelle von \(f\).
Grenzwert von \(f\) für \(x \to +\infty\)
\[\lim \limits_{x\,\to\,+\infty}f(x) = 0\]
Begründung (nicht verlangt)
Wichtiger Grenzwert
\[\lim \limits_{x \, \to \, +\infty} \frac{x^r}{e^x} = 0 \enspace (r > 0)\]
Für \(\,x \to +\infty\,\) wächst \(e^x\) „schneller" als jede Potenz \(x^r \enspace (r > 0)\).
(vgl. Merkhilfe)
\[\begin{align*}\lim \limits_{x\,\to\,+\infty}f(x) &= \lim \limits_{x\,\to\,+\infty} x \cdot e^{-\frac{1}{2}x^2+\frac{1}{2}} &&| \; a^{-n} = \frac{1}{a^n} \\[0.8em] &= \lim \limits_{x\,\to\,+\infty} \frac{\textcolor{#0087c1}{\overbrace{x}^{\to\,+\infty}}}{\textcolor{#e9b509}{\underbrace{e^{\frac{1}{2}x^2+\frac{1}{2}}}_{\to\,+\infty}}} &&| \; \lim \limits_{x \, \to \, +\infty} \frac{\textcolor{#0087c1}{x^r}}{\textcolor{#e9b509}{e^x}} = 0 \enspace (r > 0),\; \text{vgl. Merkhilfe}\\[0.8em] &= 0 \end{align*}\]
Für \(x \to +\infty\) wächst \(\textcolor{#e9b509}{e^{-\frac{1}{2}x^2+\frac{1}{2}}}\) schneller als \(\textcolor{#0087c1}{x}\).
oder:
\[\lim \limits_{x\,\to\,+\infty}f(x) = \lim \limits_{x\,\to\,+\infty}\; \textcolor{#0087c1}{\underbrace{x}_{\to\,+\infty}} \cdot \underbrace{e^{\textcolor{#cc071e}{\overbrace{-\frac{1}{2}x^2+\frac{1}{2}}^{\to\,-\infty}}}}_{\to\,0} = 0\]
