Betrachtet wird die Tangente an \(G_f\) im Punkt \((2|f(2))\). Berechnen Sie die Größe des Winkels, unter dem diese Tangente die \(x\)-Achse schneidet.
(2 BE)
Lösung zu Teilaufgabe g
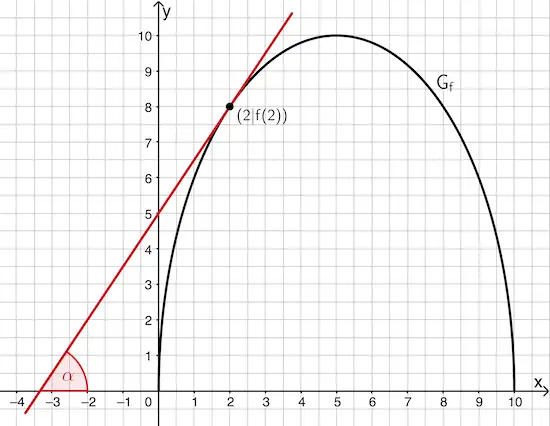
Planskizze (optional): Der Winkel, unter dem die Tangente an \(G_f\) im Punkt \((2|f(2))\) die \(x\)-Achse schneidet, entsprich dem Steigungswinkel \(\textcolor{#cc071e}{\alpha}\) der Tangente.
Der Zusammenhang zwischen der Steigung \(\textcolor{#cc071e}{m}\) der Tangente und dem Steigungswinkel \(\textcolor{#cc071e}{\alpha}\) lautet:
Steigungswinkel \(\alpha\) einer Gerade \(g \colon y = m \cdot x +t\)
\[\tan \alpha = m \qquad \alpha \neq 90^\circ\]
\[\textcolor{#cc071e}{m} = \tan{\textcolor{#cc071e}{\alpha}}\]
Für die Steigung \(\textcolor{#cc071e}{m}\) der Tangente gilt andererseits:
Anwendung der Differetialrechnung:
Steigung \(m_{T}\) einer Tangente \(T\) an den Graphen einer Funktion \(f\) im Punkt \(P\,(\,x_0\,|\,f(x_0)\,)\)
\[m_{T} = f'(x_0)\]
(vgl. Merkhilfe)
\[\textcolor{#cc071e}{m} = f'(\textcolor{#e9b509}{2})\]
Mit \(f'(x) = \dfrac{10 - 2x}{\sqrt{10x - x^2}}\) (vgl. Teilaufgabe b) ergibt sich:
\[\begin{align*}\tan{\textcolor{#cc071e}{\alpha}} &= f'(\textcolor{#e9b509}{2}) \\[0.8em] \tan{\textcolor{#cc071e}{\alpha}} &= \frac{10 - 2 \cdot \textcolor{#e9b509}{2}}{\sqrt{10 \cdot \textcolor{#e9b509}{2} - \textcolor{#e9b509}{2}^2}} \\[0.8em] \tan{\alpha} &= \frac{6}{4} = \frac{3}{2} &&| \; \text{TR:}\; \tan^{-1}(\dots) \\[1.6em] \Rightarrow \enspace \alpha &= 56{,}3^{\circ} \end{align*} \]

