Die beschriebene Spiegelung von \(G_{f}\) an der Geraden \(x = 4\) kann durch eine Spiegelung von \(G_{f}\) an der \(y\)-Achse mit anschließender Verschiebung ersetzt werden. Beschreiben Sie diese Verschiebung und geben Sie \(a, b \in \mathbb R\) an, sodass \(g(x) = f(ax + b)\) für \(x \in \; ]-\infty;8[\) gilt.
(3 BE)
Lösung zu Teilaufgabe 2b
\[g(x) = f(ax + b); \; x \in \; ]-\infty;8[\]
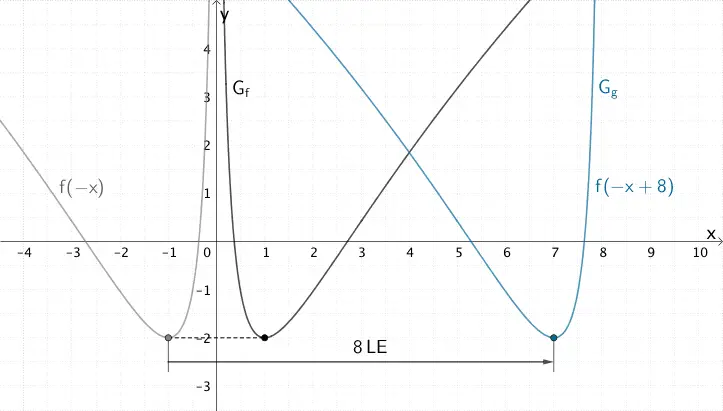
Spiegeln von Funktionsgraphen
Spiegelung an der \(x\)-Achse: \(g(x) = -f(x)\)
Spiegelung an der \(y\)-Achse: \(h(x) = f(-x)\)
\(a = -1\) entspricht einer Spiegelung von \(G_{f}\) an der \(y\)-Achse.
Verschieben von Funktionsgraphen
\[g(x) = f(x +a) + b\]
Verschiebung in \(x\)-Richtung um \(-a\), Verschiebung in \(y\)-Richtung um \(b\)
\(b = 8\) entspricht einer Verschiebung um 8 LE in Richtung der positiven \(x\)-Achse.
Sodass gilt: \(g(x) = f(-(x - 8)) = f(-x + 8)\)


