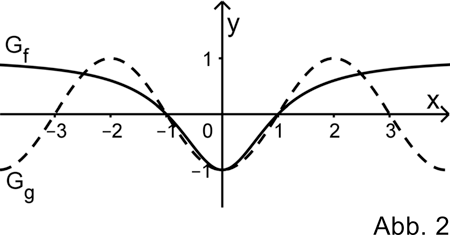
Die Abbildung 2 zeigt den Graphen \(G_{f}\) sowie den Graphen \(G_{g}\) der in \(\mathbb R\) definierten Funktion \(g \colon x \mapsto -cos(\frac{\pi}{2}x)\).
Beschreiben Sie, wie \(G_{g}\) aus dem Graphen der in \(\mathbb R\) definierten Funktion \(x \mapsto \cos{x}\) hervorgeht, und berechnen Sie durch Integration von \(g\) einen weiteren Näherungswert für \(F(1)\).
(zur Kontrolle: \(F(1) \approx -\frac{2}{\pi}\))
(5 BE)
Lösung zu Teilaufgabe 2c
\[x \mapsto \cos{x}\]
\[g(x) = -\cos\left( \frac{\pi}{2}x \right); \; D_{g} = \mathbb R\]
Allgemeine Kosinusfunktion
\[f(x) = a \cdot \cos(bx + c) + d = a \cdot \cos \left[b \left(x + \frac{c}{b} \right) \right] + d\]
\[a,b,c,d \in \mathbb R\;; \quad a,b \neq 0\;; \quad x \in \mathbb R\]
Streckung um \(a\) in \(y\)-Richtung
Streckung um \(\displaystyle \frac{1}{b}\) in \(x\)-Richtung, Periode: \(\displaystyle p = \frac{2\pi}{\vert b \vert}\)
Verschiebung um \(\displaystyle -\frac{c}{b}\) in \(x\)-Richtung
Verschiebung um \(d\) in \(y\)-Richtung
Beschreibung, wie \(G_{g}\) aus dem Graphen der Funktion \(x \mapsto \cos{x}\) hervorgeht
1. Spiegelung an der \(x\)-Achse:
Spiegeln von Funktionsgraphen
Spiegelung an der \(x\)-Achse: \(g(x) = -f(x)\)
Spiegelung an der \(y\)-Achse: \(h(x) = f(-x)\)
\[\Longrightarrow \quad \textcolor{#cc071e}{x \mapsto -\cos{x}}\]
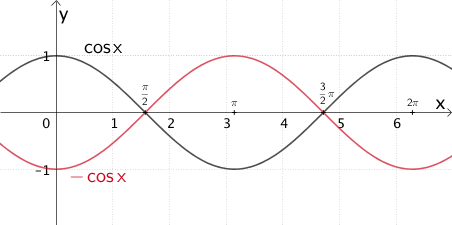
Der Graph der Funktion \(\textcolor{#cc071e}{x \mapsto -\cos{x}}\) entsteht durch Spiegelung des Graphen der in \(\mathbb R\) definierten Funktion \(x \mapsto \cos{x}\) an der \(x\)-Achse.
2. Streckung in \(x\)-Richtung:
Strecken von Funktionsgraphen
Streckung in \(\textcolor{#0087c1}{x}\)-Richtung mit Streckungsfaktor \(\textcolor{#0087c1}{k}\,\):
\[h(x) = f\left(\textcolor{#0087c1}{\frac{1}{k}} \cdot x \right), \enspace k > 0\]
Streckung in \(\textcolor{#0087c1}{x}\)-Richtung mit Streckungsfaktor \(\textcolor{#0087c1}{\dfrac{1}{k}}\):
\[h(x) = f(\textcolor{#0087c1}{k} \cdot x), \enspace k > 0\]
Streckung in \(\textcolor{#cc071e}{y}\)-Richtung mit Streckungsfaktor \(\textcolor{#cc071e}{k}\,\):
\[g(x) = \textcolor{#cc071e}{k} \cdot f(x), \enspace k > 0\]
\[\Longrightarrow \quad \textcolor{#0087c1}{-\cos{\left( \frac{\pi}{2}x \right)} = g(x)}\]
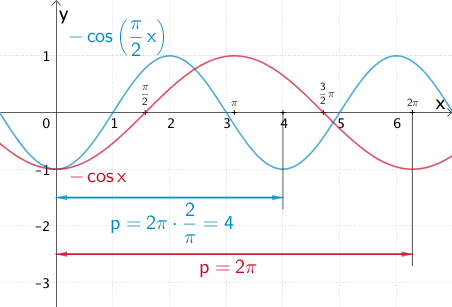
Der Graph der Funktion \(\textcolor{#0087c1}{g \colon x \mapsto -\cos{\left( \dfrac{\pi}{2}x \right)}}\) entsteht durch Streckung des Graphen der Funktion \(\textcolor{#cc071e}{x \mapsto -\cos{x}}\) in \(x\)-Richtung um den Streckungsfaktor \(\textcolor{#0087c1}{k = \dfrac{1}{\frac{\pi}{2}} = \dfrac{2}{\pi}}\).
Anmerkung:
Die Streckung in \(x\)-Richtung um den Streckungsfaktor \(\textcolor{#0087c1}{k = \dfrac{2}{\pi}}\enspace(0 < k < 1)\) bewirkt eine Stauchung.
Die Periode \(\textcolor{#cc071e}{p = 2\pi}\) wird dadurch auf \(\textcolor{#0087c1}{p = 2\pi \cdot \dfrac{2}{\pi} = 4}\) verkürzt.
Anmerkung:
Es ist ebenso möglich,
1. eine Streckung in \(x\)-Richtung um den Streckungsfaktor \(k = \dfrac{1}{\frac{\pi}{2}} = \dfrac{2}{\pi}\)
\(\Longrightarrow \quad x \mapsto \cos{\left( \frac{\pi}{2}x \right)}\) und
2. eine Spiegelung an der \(x\)-Achse
\(\Longrightarrow \quad x \mapsto -\cos{\left( \frac{\pi}{2}x \right)} = g(x)\)
zu beschreiben.
Näherungswert von \(F(1)\) durch Integration von \(g\)
Berechnung bestimmter Integrale
\[\int_{a}^{b} f(x)\,dx = [F(x)]_{a}^{b} = F(b) - F(a)\]
Dabei ist \(F\) eine beliebige Stammfunktion zu \(f\).
(vgl. Merkhilfe)
Eigenschaften des bestimmten Integrals - Integrationsregeln
Identische Integrationsgrenzen:
\[\int_{a}^{a} f(x)\,dx = 0\]
Faktorregel:
\(\displaystyle \int_{a}^{b} c \cdot f(x)\,dx = c \cdot \int_{a}^{b} f(x)\,dx\) mit \(c \in \mathbb R\)
Summenregel:
\[\int_{a}^{b} \left[f(x) \pm g(x) \right] dx = \int_{a}^{b}f(x)\,dx \pm \int_{a}^{b}g(x)\,dx\]
Vertauschungsregel:
\[\int_{a}^{b}f(x)\,dx = -\int_{b}^{a}f(x)\,dx\]
Zerlegung in Teilintervalle:
\(\displaystyle \int_{a}^{b}f(x)\,dx = \int_{a}^{c}f(x)\,dx + \int_{c}^{b}f(x)\,dx\) mit \(a \leq c \leq b\)
\[\begin{align*} F(1) &\approx \int_{0}^{1}g(t)dt \\[0.8em] &= \int_{0}^{1}-\cos{\left( \frac{\pi}{2}t \right)}dt \\[0.8em] &= \bigg[ \underbrace{-\frac{2}{\pi} \cdot \sin{\left( \frac{\pi}{2}t \right)}}_{\text{Stammfunktion}} \bigg]_{\textcolor{#89ba17}{0}}^{\textcolor{#e9b509}{1}} \\[0.8em] &= -\frac{2}{\pi} \cdot \sin{\left( \frac{\pi}{2} \cdot \textcolor{#e9b509}{1} \right)} -\left( -\frac{2}{\pi} \cdot \sin{\left( \frac{\pi}{2} \cdot \textcolor{#89ba17}{0} \right)} \right) \\[0.8em] &= -\frac{2}{\pi} \cdot \underbrace{\sin{\left( \frac{\pi}{2} \right)}}_{1} + \frac{2}{\pi} \cdot \underbrace{\sin{0}}_{0} \\[0.8em] &= -\frac{2}{\pi} \end{align*}\]
Ausführliche Erklärung (nicht verlangt)
Im Bereich \(0 \leq x \leq 1\) gleicht der Verlauf des Graphen \(G_{g}\) näherungsweise dem Verlauf des Graphen \(G_{f}\).
Die Nullstellen \(x_{1} = -1\) und \(x_{2} = 1\) von \(f\) sind zugleich Nullstellen von \(g\). Denn die Nullstellen der Kosinusfunktion \(x \mapsto \cos{x}\) sind \((2k + 1) \cdot \frac{\pi}{2}\) mit \(k \in \mathbb Z\) (ungeradzahlige Vielfache von \(\frac{\pi}{2}\)). Folglich sind \(2k + 1\) mit \(k \in \mathbb Z\) (ungerade ganze Zahlen) die Nullstellen der Funktion \(g \colon x \mapsto -\cos{\left( \frac{\pi}{2}x \right)}\).
Deshalb lässt sich durch Integration von \(g\) ein Näherungswert für \(F(1)\) berechnen.
\[F(1) = \int_{0}^{1}f(t)dt \approx \textcolor{#0087c1}{\int_{0}^{1}g(t)dt}\]
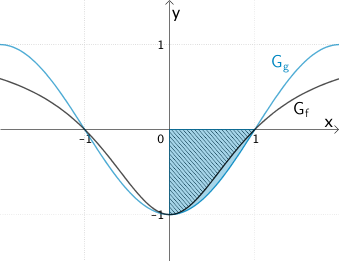
Für die Berechnung des bestimmten Integrals \(\displaystyle \int_{0}^{1}g(t)dt\) wird eine Stammfunktion der Integrandenfunktion \(g\) benötigt.
Die Menge aller Stammfunktionen von \(g\) ist gegeben durch das unbestimmte Integral \(\displaystyle \int g(t)dt = \int -\cos{\left( \frac{\pi}{2}t \right)}dt\).
Mithilfe der unbestimmten Integrale
\(\textcolor{#cc071e}{\displaystyle \int \cos{x} \, dx = \sin{x} + C}\) und
\(\textcolor{#0087c1}{\displaystyle \int f(ax + b) \, dx = \frac{1}{a} \cdot F(ax + b) + C}\)
ergibt sich:
Wichtige unbestimmte Integrale (\(C \in \mathbb R\), vgl. Merkhilfe)
\[\int x^{r} dx = \frac{x^{r + 1}}{r + 1} + C \quad (r \neq - 1)\]
\[\int \frac{1}{x}\,dx = \ln{\vert x \vert} + C\]
\[\int \sin{x} \, dx = -\cos{x} + C\]
\[\int \cos{x} \, dx = \sin{x} + C\]
\[\int e^{x} dx = e^{x} + C\]
\[\int \ln{x}\, dx = -x + x \cdot \ln{x} + C\]
\[\int \frac{f'(x)}{f(x)} dx = \ln{\vert f(x) \vert} + C\]
\[\int f'(x) \cdot e^{f(x)} dx = e^{f(x)} + C\]
\(\displaystyle \int f(ax + b) \, dx = \frac{1}{a} \cdot F(ax + b) + C\), wobei \(F\) eine Stammfunktion von \(f\) ist.
Es gilt die Faktorregel und die Summenregel:
\(\displaystyle \int c \cdot f(x)\,dx = c \cdot \int f(x)\,dx\) mit \(c \in \mathbb R\)
\( \displaystyle \int \left[f(x) \pm g(x) \right] dx = \int f(x)\,dx \pm \int g(x)\,dx\)
\[\begin{align*}\int -\textcolor{#cc071e}{\cos}{\left(\textcolor{#0087c1}{\frac{\pi}{2}t}\right)}dt &= -\textcolor{#0087c1}{\frac{1}{\frac{\pi}{2}}} \cdot \textcolor{#cc071e}{\sin}{\left( \textcolor{#0087c1}{\frac{\pi}{2}t}\right)} + C \\[0.8em] &= -\frac{2}{\pi} \cdot \sin{\left( \frac{\pi}{2}t\right)} + C\end{align*}\]
Somit ist \(G \colon t \mapsto -\frac{2}{\pi} \cdot \sin{\left( \dfrac{\pi}{2}t \right)}\) eine Stammfunktion der Integrandenfunktion \(g \colon t \mapsto -\cos{\left( \dfrac{\pi}{2}t \right)}\) (für \(C = 0\)) und es folgt:
Berechnung bestimmter Integrale
\[\int_{a}^{b} f(x)\,dx = [F(x)]_{a}^{b} = F(b) - F(a)\]
Dabei ist \(F\) eine beliebige Stammfunktion zu \(f\).
(vgl. Merkhilfe)
Eigenschaften des bestimmten Integrals - Integrationsregeln
Identische Integrationsgrenzen:
\[\int_{a}^{a} f(x)\,dx = 0\]
Faktorregel:
\(\displaystyle \int_{a}^{b} c \cdot f(x)\,dx = c \cdot \int_{a}^{b} f(x)\,dx\) mit \(c \in \mathbb R\)
Summenregel:
\[\int_{a}^{b} \left[f(x) \pm g(x) \right] dx = \int_{a}^{b}f(x)\,dx \pm \int_{a}^{b}g(x)\,dx\]
Vertauschungsregel:
\[\int_{a}^{b}f(x)\,dx = -\int_{b}^{a}f(x)\,dx\]
Zerlegung in Teilintervalle:
\(\displaystyle \int_{a}^{b}f(x)\,dx = \int_{a}^{c}f(x)\,dx + \int_{c}^{b}f(x)\,dx\) mit \(a \leq c \leq b\)
\[\begin{align*} F(1) &\approx \int_{0}^{1}g(t)dt \\[0.8em] &= \int_{0}^{1}-\cos{\left( \frac{\pi}{2}t \right)}dt \\[0.8em] &= \bigg[ \underbrace{-\frac{2}{\pi} \cdot \sin{\left( \frac{\pi}{2}t \right)}}_{\text{Stammfunktion}} \bigg]_{\textcolor{#89ba17}{0}}^{\textcolor{#e9b509}{1}} \\[0.8em] &= -\frac{2}{\pi} \cdot \sin{\left( \frac{\pi}{2} \cdot \textcolor{#e9b509}{1} \right)} -\left( -\frac{2}{\pi} \cdot \sin{\left( \frac{\pi}{2} \cdot \textcolor{#89ba17}{0} \right)} \right) \\[0.8em] &= -\frac{2}{\pi} \cdot \underbrace{\sin{\left( \frac{\pi}{2} \right)}}_{1} + \frac{2}{\pi} \cdot \underbrace{\sin{0}}_{0} \\[0.8em] &= -\frac{2}{\pi} \end{align*}\]


