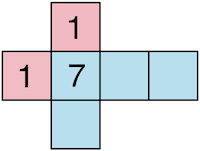
Die Abbildung zeigt das Netz eines Würfels, von dem nur drei Seiten beschriftet sind.
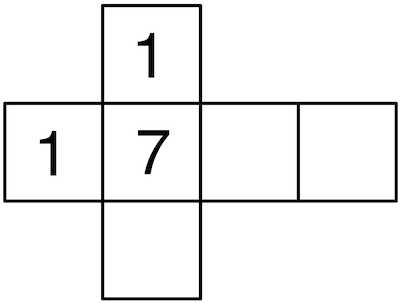
Der Würfel wird so lange geworfen, bis die Zahl 1 zum ersten Mal erzielt wird. Berechnen Sie die Wahrscheinlichkeit dafür, dass genau viermal gewürfelt wird.
(2 BE)
Lösung zu Teilaufgabe a
Laplace-Wahrscheinlichkeit eines Ereignisses \(A\)
\[P(A) = \frac{\vert A \vert}{\vert \Omega \vert} = \frac{\text{Anzahl der für} \; A \; \text{günstigen Ergebnisse}}{\text{Anzahl der möglichen Ergebnisse}}\]
Voraussetzung: Alle Ergebnisse (alle Versuchsausgänge) des betrachteten Zufallsexperiments sind gleichwahrscheinlich (Laplace-Experiment).
\[P(\textcolor{#cc071e}{\text{„Zahl ist 1"}}) = \frac{\textcolor{#cc071e}{2}}{6} = \frac{1}{3}\]
\[P(\textcolor{#0087c1}{\text{„Zahl ist nicht 1"}}) = \frac{\textcolor{#0087c1}{4}}{6} = \frac{2}{3}\]
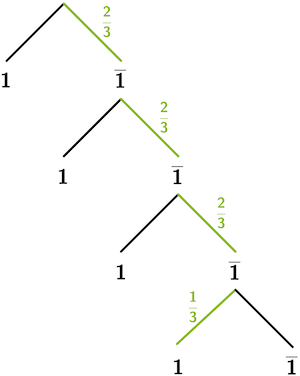
Veranschaulichung des Ereignisses „Es wird genau viermal gewürfelt" mithilfe eines Baumdiagramms (optional)
Mithilfe der 1. Pfadregel ergibt sich:
Pfadregeln
Verzweigungsregel (Knotenregel)
Die Summe der Wahrscheinlichkeiten an den Ästen, die von einem Knoten ausgehen, ist gleich eins.
1. Pfadregel (Produktregel)
Die Wahrscheinlichkeit eines Ergebnisses ist gleich dem Produkt der Wahrscheinlichkeiten entlang des Pfades, der zu dem Ergebnis führt.
2. Pfadregel (Summenregel)
Die Wahrscheinlichkeit eines Ereignisses ist gleich der Summe der Wahrscheinlichkeiten der Ergebnisse, die zu diesem Ereignis gehören.
\[\begin{align*}P(\text{„genau viermal würfeln"}) &= P(\{\overline{1};\overline{1};\overline{1};1\}) \\[0.8em] &= \textcolor{#89ba17}{\frac{2}{3}} \cdot \textcolor{#89ba17}{\frac{2}{3}} \cdot \textcolor{#89ba17}{\frac{2}{3}} \cdot \textcolor{#89ba17}{\frac{1}{3}} \\[0.8em] &= \left( \frac{2}{3} \right)^{3} \cdot \frac{1}{3} \\[0.8em] &= \frac{8}{81}\end{align*}\]


