Eine Kugel besitzt den Mittelpunkt \(M\,(-3|2|7)\). Der Punkt \(P\,(3|4|4)\) liegt auf der Kugel.

Der Punkt \(Q\) liegt ebenfalls auf der Kugel, die Strecke \([PQ]\) verläuft durch deren Mittelpunkt. Ermitteln Sie die Koordinaten von \(Q\).

(3 BE)

Lösung zu Teilaufgabe 2a

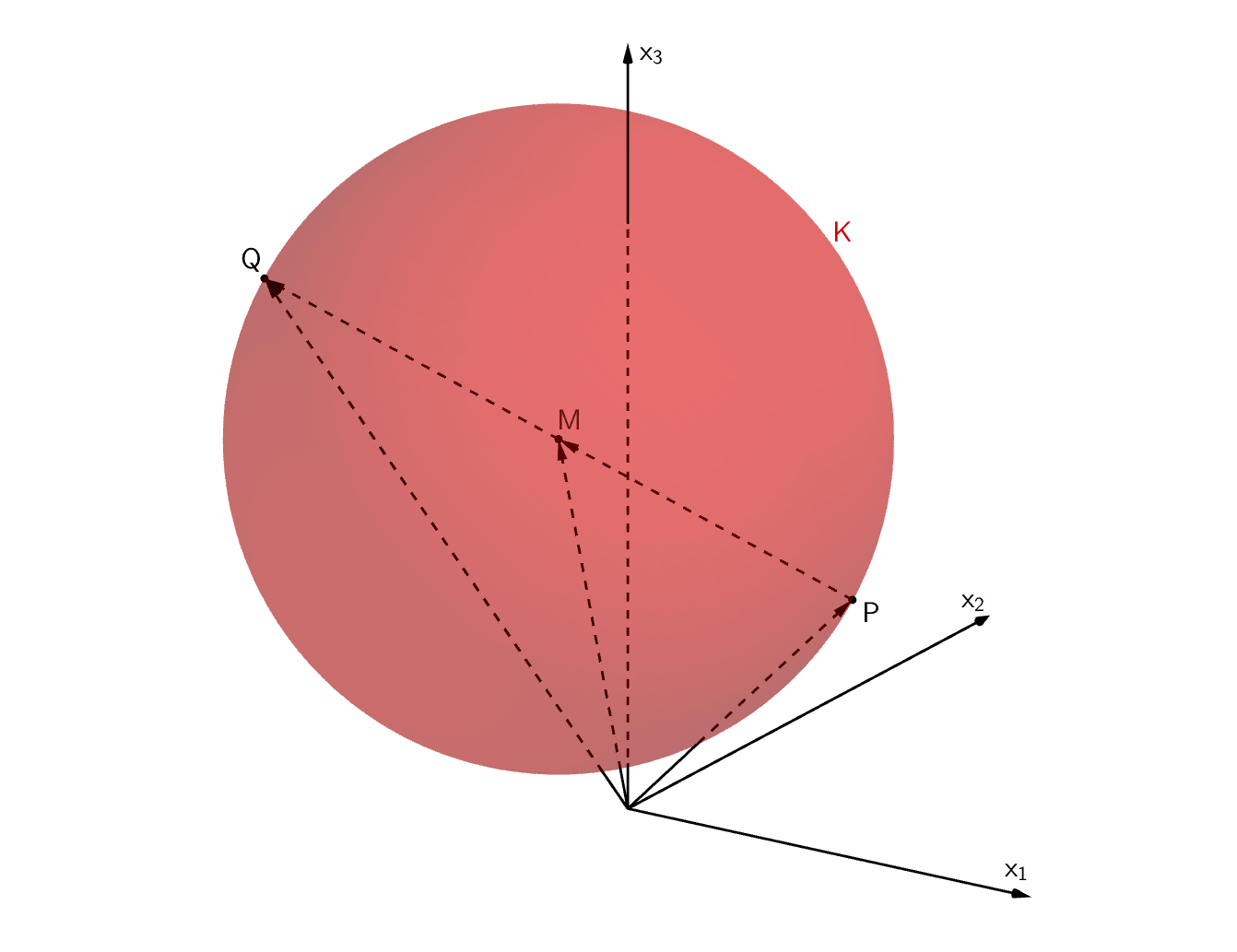
Kugel \(K\) mit Mittelpunkt \(M\), \(P \in K\), \(Q \in K\), \(M \in [PQ]\)

Die Koordinaten des Punktes \(Q\) lassen sich durch Vektoraddition ermitteln.

\[M\,(-3|2|7)\,, \enspace P\,(3|4|4)\]

\[\begin{align*} \overrightarrow{Q} &= \overrightarrow{M} + \overrightarrow{MQ} \\[0.8em] &= \overrightarrow{M} + \overrightarrow{PM} \\[0.8em] &= \overrightarrow{M} + \bigg( \overrightarrow{M} - \overrightarrow{P} \bigg) \\[0.8em] &= \overrightarrow{M} + \overrightarrow{M} - \overrightarrow{P} \\[0.8em] &= \begin{pmatrix} -3 \\ 2 \\ 7 \end{pmatrix} + \begin{pmatrix} -3 \\ 2 \\ 7 \end{pmatrix} - \begin{pmatrix} 3 \\ 4 \\ 4 \end{pmatrix} \\[0.8em] &= \begin{pmatrix} -9 \\ 0 \\ 10 \end{pmatrix} \end{align*}\]

\[\Longrightarrow \quad Q\,(-9|0|10)\]

oder :

\[\begin{align*} \overrightarrow{Q} &= \overrightarrow{P} + 2 \cdot \overrightarrow{PM} \\[0.8em] &= \overrightarrow{P} + 2 \cdot \bigg( \overrightarrow{M} - \overrightarrow{P} \bigg) \\[0.8em] &= \begin{pmatrix} 3 \\ 4 \\ 4 \end{pmatrix} + 2 \cdot \left[ \begin{pmatrix} -3 \\ 2 \\ 7 \end{pmatrix} - \begin{pmatrix} 3 \\ 4 \\ 4 \end{pmatrix} \right] \\[0.8em] &= \begin{pmatrix} 3 \\ 4 \\ 4 \end{pmatrix} + 2 \cdot \begin{pmatrix} -6 \\ -2 \\ 3 \end{pmatrix} \\[0.8em] &= \begin{pmatrix} -9 \\ 0 \\ 10 \end{pmatrix} \end{align*}\]

\[\Longrightarrow \quad Q\,(-9|0|10)\]