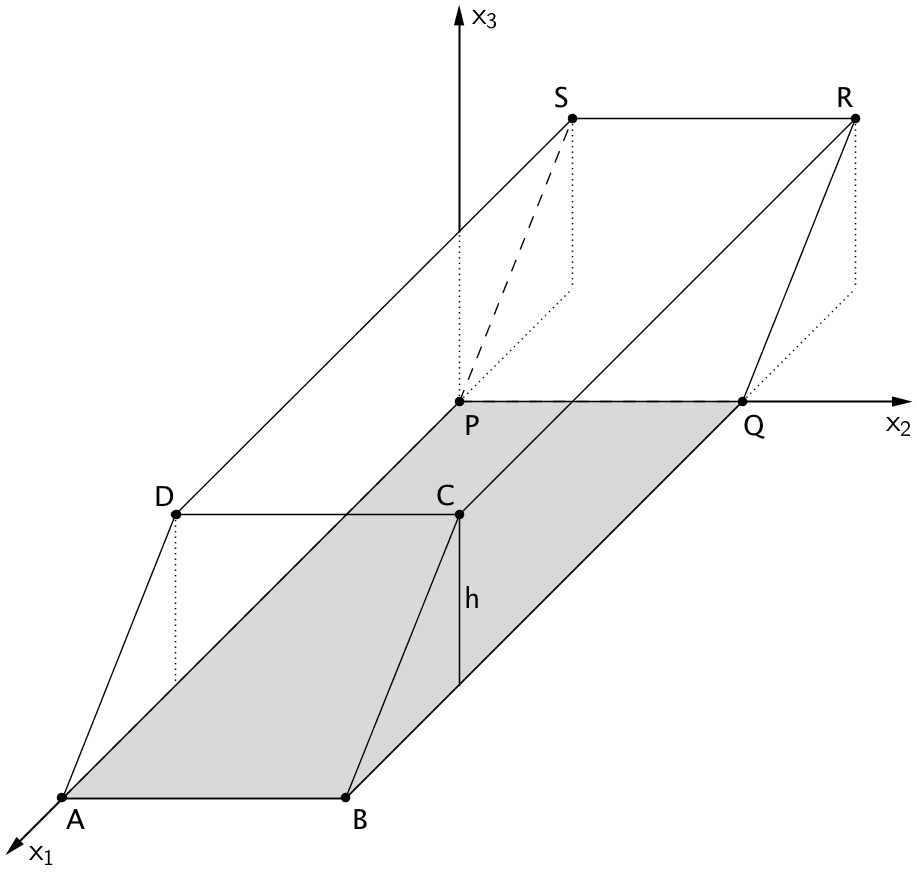
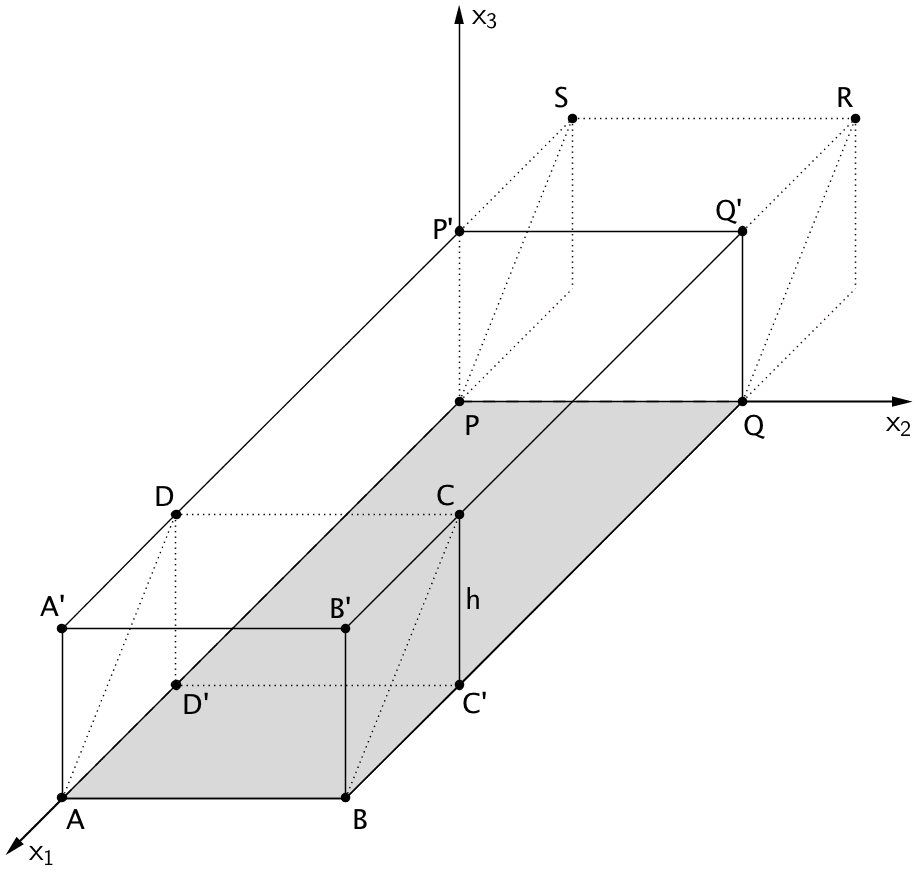
Ein Kubikmeter des verwendeten Betons besitzt eine Masse von 2,1 t. Berechnen Sie die Masse des Grundkörpers.
(3 BE)
Lösung zu Teilaufgabe f
\[1\,\text{m}^3 \, \mathrel{\widehat{=}} \, 2{,}1\,\text{t}\]
1. Lösungsansatz: \(V = G \cdot h\) (siehe Teilaufgabe e)
Das Volumne des Spats \(ABCDPQRS\) lässt sich mithilfe der Formel \(V = G \cdot h\) berechnen, wobei \(G\) der Flächeninhalt des Rechtecks \(ABQP\) und \(h\) die zugehörige Höhe des Spats ist (siehe Teilaufgabe e).
Flächeninhalt \(G\) des Rechtecks \(ABQP\) berechnen:
Betrag eines Vektors
\[ \vert \overrightarrow{a} \vert = \sqrt{\overrightarrow{a} \circ \overrightarrow{a}} = \sqrt{{a_1}^2 + {a_2}^2 + {a_3}^2}\]
(vgl. Merkhilfe)
\[G = \overline{AB} \cdot \overline{AP} = \vert \overrightarrow{AB} \vert \cdot \vert \overrightarrow{AP} \vert\]
\(\displaystyle \overrightarrow{AB} = \begin{pmatrix} 0 \\ 10 \\ 0 \end{pmatrix}\) (siehe Teilaufgabe a)
\[\overrightarrow{AP} = \overrightarrow{P} - \overrightarrow{A} = \begin{pmatrix} 0 \\ 0 \\ 0 \end{pmatrix} - \begin{pmatrix} 28 \\ 0 \\ 0 \end{pmatrix} = \begin{pmatrix} -28 \\ 0 \\ 0 \end{pmatrix}\]
\[\begin{align*} G &= \vert \overrightarrow{AB} \vert \cdot \vert \overrightarrow{AP} \vert \\[0.8em] &= \left| \begin{pmatrix} 0 \\ 10 \\ 0 \end{pmatrix} \right| \cdot \left| \begin{pmatrix} -28 \\ 0 \\ 0 \end{pmatrix} \right| \\[0.8em] &= \sqrt{0^2 + 10^2 + 0^2} \cdot \sqrt{(-28)^2 + 0^2 + 0^2} \\[0.8em] &= 10 \cdot 28 \\[0.8em] &= 280 \end{align*}\]
Alternative: Flächeninhalt \(G\) mithilfe des Vektorprodukts berechnen:
Vektorprodukt (Kreuzprodukt)
Das Vektorprodukt \(\overrightarrow{a} \times \overrightarrow{b}\) zweier Vektoren \(\overrightarrow{a}\) und \(\overrightarrow{b}\) erzeugt einen neuen Vektor \(\overrightarrow{c} = \overrightarrow{a} \times \overrightarrow{b}\) mit den Eigenschaften:
\(\overrightarrow{c}\) ist sowohl zu \(\overrightarrow{a}\) als auch zu \(\overrightarrow{b}\) senkrecht.
\[\overrightarrow{c} = \overrightarrow{a} \times \overrightarrow{b} \quad \Longrightarrow \quad \overrightarrow{c} \perp \overrightarrow{a}, \enspace \overrightarrow{c} \perp \overrightarrow{b}\]
Der Betrag des Vektorprodukts zweier Vektoren \(\overrightarrow{a}\) und \(\overrightarrow{b}\) ist gleich dem Produkt aus den Beträgen der Vektoren \(\overrightarrow{a}\) und \(\overrightarrow{b}\) und dem Sinus des von ihnen eingeschlossenen Winkels \(\varphi\).
\[\vert \overrightarrow{a} \times \overrightarrow{b} \vert = \vert \overrightarrow{a} \vert \cdot \vert \overrightarrow{b} \vert \cdot \sin{\varphi} \quad (0^{\circ} \leq \varphi \leq 180^{\circ})\]
Die Vektoren \(\overrightarrow{a}\), \(\overrightarrow{b}\) und \(\overrightarrow{c}\) bilden in dieser Reihenfolge ein Rechtssystem. Rechtehandregel: Weist \(\overrightarrow{a}\) in Richtung des Daumens und \(\overrightarrow{b}\) in Richtung des Zeigefingers, dann weist \(\overrightarrow{c} = \overrightarrow{a} \times \overrightarrow{b}\) in Richtung des Mittelfingers.
Berechnung eines Vektorprodukts im \(\boldsymbol{\mathbb R^{3}}\) (vgl. Merkhilfe)
\[\overrightarrow{a} \times \overrightarrow{b} = \begin {pmatrix} a_1 \\ a_2 \\ a_3 \end {pmatrix} \times \begin {pmatrix} b_1 \\ b_2 \\ b_3 \end {pmatrix} = \begin {pmatrix} a_2 \cdot b_3 - a_3 \cdot b_2 \\ a_3 \cdot b_1 - a_1 \cdot b_3 \\ a_1 \cdot b_2 - a_2 \cdot b_1 \end {pmatrix}\]
\[\begin{align*} G &= \vert \overrightarrow{AB} \times \overrightarrow{AP} \vert \\[0.8em] &= \left| \begin{pmatrix} 0 \\ 10 \\ 0 \end{pmatrix} \times \begin{pmatrix} -28 \\ 0 \\ 0 \end{pmatrix} \right| \\[0.8em] &= \left| \begin{pmatrix} 10 & \cdot & 0 & - & 0 & \cdot & 0 \\ 0 & \cdot & (-28) & - & 0 & \cdot & 0 \\ 0 & \cdot & 0 & - & 10 & \cdot & (-28)\end{pmatrix} \right| \\[0.8em] &= \left| \begin{pmatrix} 0 \\ 0 \\ 280 \end{pmatrix} \right| \\[0.8em] &= \sqrt{0^2 + 0^2 + 280^2} \\[0.8em] &= 280 \end{align*}\]
Höhe \(h\) des Spats bestimmen:
\(D\,(20|0|6)\,, \enspace C\,(20|10|6)\enspace\) (siehe Teilaufgabe a)
\[\left. \begin{align*} DCRS &\parallel ABQP \\[0.8em] ABQP &\subset x_1x_2\text{-Ebene} \end{align*} \right\} \enspace \Rightarrow \enspace h = x_{3_D} = x_{3_C} = 6\]
Volumen \(V\) des Spats \(ABCDPQRS\) berechnen:
\[V = G \cdot h = 280 \cdot 6 = 1680\]
Der Volumneinhalt des Spats \(ABCDPQRS\) beträgt 1680 VE (Volumeneinheiten).
\[1\,\text{LE} \, \mathrel{\widehat{=}} \, 0{,}1\,\text{m} \quad \Longrightarrow \quad 1\,\text{VE} \, \mathrel{\widehat{=}} \, 0{,}1^3\,\text{m}^3 = 0{,}001\,\text{m}^3\]
\[V = (1680 \cdot 0{,}001)\,\text{m}^3 = 1{,}68\,\text{m}^3\]
Der Volumneinhalt des Spats \(ABCDPQRS\) beträgt 1,68 m³.
Masse des Grundkörpers berechnen:
\[1\,\text{m}^3 \, \mathrel{\widehat{=}} \, 2{,}1\,\text{t}\]
\[m = (1{,}68 \cdot 2{,}1)\,\text{t} = 3{,}528\,\text{t} = 3528\,\text{kg}\]
2. Lösungsansatz: Anwenden des Spatprodukts
![\[1\,\text{m}^3 \, \mathrel{\widehat{=}} \, 2{,}1\,\text{t}\] Drei linear unabhängige Vektoren spannen den Spat ABCDPQRS auf.](/images/stories/B2013_G_I/B2013_G_I_f_03.png)
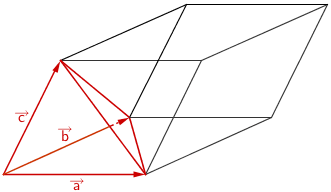
Die drei linear unabhängigen Vektoren \(\overrightarrow{AB}\,\), \(\overrightarrow{AD}\) und \(\overrightarrow{AP}\) spannen den Spat \(ABCDPQRS\) auf.
Anwendung des Vekorprodukts - Spatprodukt (vgl. Merkhilfe)
Volumen eines Spats
\[V_{\text{Spat}} = \left| \left( \overrightarrow{a} \times \overrightarrow{b} \right) \circ \overrightarrow{c} \; \right|\]
Volumen einer dreiseitigen Pyramide
\[V_{\text{Pyramide}} = \frac{1}{6} \left| \left( \overrightarrow{a} \times \overrightarrow{b} \right) \circ \overrightarrow{c} \; \right|\]
\[V = \left| \left( \overrightarrow{AB} \times \overrightarrow{AP} \right) \circ \overrightarrow{AD}\;\right|\]
\(\displaystyle \overrightarrow{AB} = \begin{pmatrix} 0 \\ 10 \\ 0 \end{pmatrix}; \; \displaystyle \overrightarrow{AD} = \begin{pmatrix} -8 \\ 0 \\ 6 \end{pmatrix}; \; \displaystyle \overrightarrow{AP} = \begin{pmatrix} -28 \\ 0 \\ 0 \end{pmatrix}\) (siehe Teilaufgabe a bzw. 1. Lösungsansatz)
Volumen \(V\) des Spats \(ABCDPQRS\) berechnen:
Vektorprodukt (Kreuzprodukt)
Das Vektorprodukt \(\overrightarrow{a} \times \overrightarrow{b}\) zweier Vektoren \(\overrightarrow{a}\) und \(\overrightarrow{b}\) erzeugt einen neuen Vektor \(\overrightarrow{c} = \overrightarrow{a} \times \overrightarrow{b}\) mit den Eigenschaften:
\(\overrightarrow{c}\) ist sowohl zu \(\overrightarrow{a}\) als auch zu \(\overrightarrow{b}\) senkrecht.
\[\overrightarrow{c} = \overrightarrow{a} \times \overrightarrow{b} \quad \Longrightarrow \quad \overrightarrow{c} \perp \overrightarrow{a}, \enspace \overrightarrow{c} \perp \overrightarrow{b}\]
Der Betrag des Vektorprodukts zweier Vektoren \(\overrightarrow{a}\) und \(\overrightarrow{b}\) ist gleich dem Produkt aus den Beträgen der Vektoren \(\overrightarrow{a}\) und \(\overrightarrow{b}\) und dem Sinus des von ihnen eingeschlossenen Winkels \(\varphi\).
\[\vert \overrightarrow{a} \times \overrightarrow{b} \vert = \vert \overrightarrow{a} \vert \cdot \vert \overrightarrow{b} \vert \cdot \sin{\varphi} \quad (0^{\circ} \leq \varphi \leq 180^{\circ})\]
Die Vektoren \(\overrightarrow{a}\), \(\overrightarrow{b}\) und \(\overrightarrow{c}\) bilden in dieser Reihenfolge ein Rechtssystem. Rechtehandregel: Weist \(\overrightarrow{a}\) in Richtung des Daumens und \(\overrightarrow{b}\) in Richtung des Zeigefingers, dann weist \(\overrightarrow{c} = \overrightarrow{a} \times \overrightarrow{b}\) in Richtung des Mittelfingers.
Berechnung eines Vektorprodukts im \(\boldsymbol{\mathbb R^{3}}\) (vgl. Merkhilfe)
\[\overrightarrow{a} \times \overrightarrow{b} = \begin {pmatrix} a_1 \\ a_2 \\ a_3 \end {pmatrix} \times \begin {pmatrix} b_1 \\ b_2 \\ b_3 \end {pmatrix} = \begin {pmatrix} a_2 \cdot b_3 - a_3 \cdot b_2 \\ a_3 \cdot b_1 - a_1 \cdot b_3 \\ a_1 \cdot b_2 - a_2 \cdot b_1 \end {pmatrix}\]
Skalarprodukt
Unter dem Skalarprodukt \(\overrightarrow{a} \circ \overrightarrow{b}\) zweier Vektoren \(\overrightarrow{a}\) und \(\overrightarrow{b}\) versteht man das Produkt aus den Beträgen der beiden Vektoren und dem Kosinus des von den Vektoren eingeschlossenen Winkels \(\varphi\).
\[\overrightarrow{a} \circ \overrightarrow{b} = \vert \overrightarrow{a} \vert \cdot \vert \overrightarrow{b} \vert \cdot \cos{\varphi} \quad (0^{\circ} \leq \varphi \leq 180^{\circ})\]
Berechnung eines Skalarprodukts im \(\boldsymbol{\mathbb R^{3}}\) (vgl. Merkhilfe)
\[\overrightarrow{a} \circ \overrightarrow{b} = \begin{pmatrix} a_{1} \\ a_{2} \\ a_{3} \end{pmatrix} \circ \begin{pmatrix} b_{1} \\ b_{2} \\ b_{3} \end{pmatrix} = a_{1}b_{1} + a_{2}b_{2} + a_{3}b_{3}\]
\[\begin {align*} V &= \left| \left( \overrightarrow{AB} \times \overrightarrow{AP} \right) \circ \overrightarrow{AD}\;\right| \\[0.8em] &= \left| \left[ \begin {pmatrix} 0 \\ 10 \\ 0 \end {pmatrix} \times \begin {pmatrix} -28 \\ 0 \\ 0 \end {pmatrix} \right] \circ \begin {pmatrix} -8 \\ 0 \\ 6 \end {pmatrix} \right| \\[0.8em] &= \left| \begin {pmatrix} 10 & \cdot & 0 & - & 0 & \cdot & 0 \\ 0 & \cdot & (-28) & - & 0 & \cdot & 0 \\ 0 & \cdot & 0 & - & 10 & \cdot & (-28) \end {pmatrix} \circ \begin {pmatrix} -8 \\ 0 \\ 6 \end {pmatrix} \right| \\[0.8em] &= \left| \begin {pmatrix} 0 \\ 0 \\ 280 \end {pmatrix} \circ \begin {pmatrix} -8 \\ 0 \\ 6 \end {pmatrix} \right| \\[0.8em] &= \left| 0 \cdot (-8) + 0 \cdot 0 + 280 \cdot 6 \right| \\[0.8em] &= 1680 \end {align*}\]
Der Volumneinhalt des Spats \(ABCDPQRS\) beträgt 1680 VE (Volumeneinheiten).
\[1\,\text{LE} \, \mathrel{\widehat{=}} \, 0{,}1\,\text{m} \quad \Longrightarrow \quad 1\,\text{VE} \, \mathrel{\widehat{=}} \, 0{,}1^3\,\text{m}^3 = 0{,}001\,\text{m}^3\]
\[V = (1680 \cdot 0{,}001)\,\text{m}^3 = 1{,}68\,\text{m}^3\]
Der Volumneinhalt des Spats \(ABCDPQRS\) beträgt 1,68 m³.
Masse des Grundkörpers berechnen:
\[1\,\text{m}^3 \, \mathrel{\widehat{=}} \, 2{,}1\,\text{t}\]
\[m = (1{,}68 \cdot 2{,}1)\,\text{t} = 3{,}528\,\text{t} = 3528\,\text{kg}\]