Ein Großhändler bietet Samenkörner für Salatgurken in zwei Qualitätsstufen an. Ein Samenkorn der höheren Qualität A keimt mit einer Wahrscheinlichkeit von 95 %, eines der Qualität B mit einer Wahrscheinlichkeit von 70 %. Ein Anbaubetrieb kauft Samenkörner beider Qualitätsstufen, 65 % aller gekauften Samenkörner sind von der Qualität A.
In einem Gedankenexperiment werden die eingekauften Samenkörner zusammengeschüttet und gemischt. Bestimmen Sie mithilfe eines beschrifteten Baumdiagramms
α) die Wahrscheinlichkeit dafür, dass ein zufällig ausgewähltes Samenkorn keimt;
β) die Wahrscheinlichkeit dafür, dass ein zufällig ausgewähltes Samenkorn, das nach der Saat keimt, von der Qualität B ist.
(5 BE)
Lösung zu Teilaufgabe a
Baumdiagramm, Pfadregeln, Bedingte Wahrscheinlichkeit
Ereignisse festlegen:
\(A\): „Samenkorn ist von der Qualität A."
\(B\): „Samenkorn ist von der Qualität B." (entspricht \(\overline{A}\))
\(K\): „Samenkorn keimt."
\(\overline{K}\): „Samenkorn keimt nicht."
Gegeben ist die Wahrscheinlichkeit \(P(A) = 0{,}65\) sowie die bedingten Wahrscheinlichkeiten \(P_{A}(K) = 0{,}95\) und \(P_{B}(K) = 0{,}7\).
α) Wahrscheinlichkeit dafür, dass ein zufällig ausgewähltes Samenkorn keimt
Da die Wahrscheinlichkeit \(P(A)\) gegeben ist, unterscheidet die erste Stufe des zu erstellenden Baumdiagramms die Ereignisse \(A\) und \(B\).
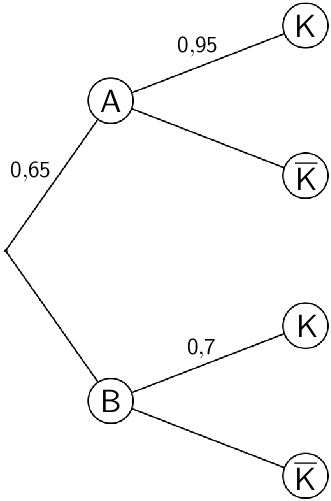
Baumdiagramm mit den Eintragungen der gegebenen Wahrscheinlichkeiten \(P(A) = 0{,}65\), \(P_{A}(K) = 0{,}95\) und \(P_{B}(K) = 0{,}7\)
Die Wahrscheinlichkeit \(P(K)\) lässt sich mithilfe der Knotenregel sowie der 1. und 2. Pfadregel berechnen.
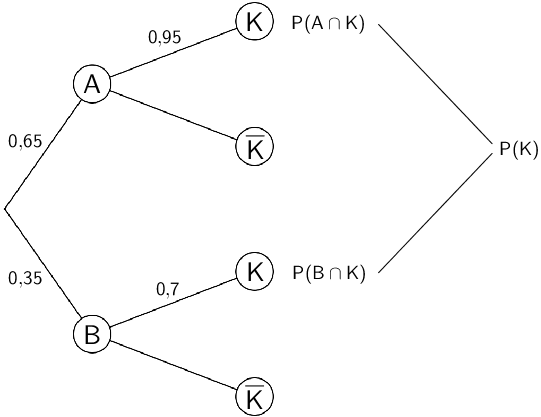
Knotenregel anwenden:
Pfadregeln
Verzweigungsregel (Knotenregel)
Die Summe der Wahrscheinlichkeiten an den Ästen, die von einem Knoten ausgehen, ist gleich eins.
1. Pfadregel (Produktregel)
Die Wahrscheinlichkeit eines Ergebnisses ist gleich dem Produkt der Wahrscheinlichkeiten entlang des Pfades, der zu dem Ergebnis führt.
2. Pfadregel (Summenregel)
Die Wahrscheinlichkeit eines Ereignisses ist gleich der Summe der Wahrscheinlichkeiten der Ergebnisse, die zu diesem Ereignis gehören.
\[P(B) = 1 - P(A) = 1 - 0{,}65 = 0{,}35\]
Wahrscheinlichkeit \(P(K)\) mithilfe der 1. und 2. Pfadregel berechnen:
Pfadregeln
Verzweigungsregel (Knotenregel)
Die Summe der Wahrscheinlichkeiten an den Ästen, die von einem Knoten ausgehen, ist gleich eins.
1. Pfadregel (Produktregel)
Die Wahrscheinlichkeit eines Ergebnisses ist gleich dem Produkt der Wahrscheinlichkeiten entlang des Pfades, der zu dem Ergebnis führt.
2. Pfadregel (Summenregel)
Die Wahrscheinlichkeit eines Ereignisses ist gleich der Summe der Wahrscheinlichkeiten der Ergebnisse, die zu diesem Ereignis gehören.
\[\begin{align*} P(K) &= P(A \cap K) + P(B \cap K) \\[0.8em] &= \underbrace{\underbrace{P(A) \cdot P_{A}(K)}_{\large{\text{1. Pfadregel}}} + \underbrace{P(B) \cdot P_{B}(K)}_{\large{\text{1. Pfadregel}}}}_{\large{\text{2. Pfadregel}}} \\[0.8em] &= 0{,}65 \cdot 0{,}95 + 0{,}35 \cdot 0{,}7 \\[0.8em] &= 0{,}8625 \\[0.8em] &= 86{,}25\,\% \end{align*}\]
β) Wahrscheinlichkeit dafür, dass ein zufällig ausgewähltes Samenkorn, das nach der Saat keimt, von der Qualität B ist
Gesucht ist die bedingte Wahrscheinlichkeit \(P_{K}(B)\).
Bedingte Wahrscheinlichkeit
Die Wahrscheinlichkeit für das Eintreten des Ereignisses \(B\) unter der Voraussetzung oder der Bedingung, dass das Ereignis \(A\) bereits eingetreten ist, heißt bedingte Wahrscheinlichkeit von \(\boldsymbol{B}\) unter der Bedingung \(\boldsymbol{A}\) und wird durch die Schreibweise \(P_{A}(B)\) gekennzeichnet.
Es gilt: \(P_{A}(B) = \dfrac{P(A \cap B)}{P(A)} \quad (P(A) \neq 0)\)
(vgl. Merkhilfe)
\[P_{K}(B) = \frac{P(B \cap K)}{P(K)}\]
Die Wahrscheinlichkeit \(P(K)\) wurde unter α) bereits berechnet. Die Wahrscheinlichkeit \(P(B \cap K)\) ergibt sich mithilfe der 1. Pfadregel.
\[P(K) = 0{,}8625\]
Pfadregeln
Verzweigungsregel (Knotenregel)
Die Summe der Wahrscheinlichkeiten an den Ästen, die von einem Knoten ausgehen, ist gleich eins.
1. Pfadregel (Produktregel)
Die Wahrscheinlichkeit eines Ergebnisses ist gleich dem Produkt der Wahrscheinlichkeiten entlang des Pfades, der zu dem Ergebnis führt.
2. Pfadregel (Summenregel)
Die Wahrscheinlichkeit eines Ereignisses ist gleich der Summe der Wahrscheinlichkeiten der Ergebnisse, die zu diesem Ereignis gehören.
\[\begin{align*}P_{K}(B) &= \frac{P(B \cap K)}{P(K)} \\[0.8em] &= \frac{\overbrace{P(B) \cdot P_{B}(K)}^{\large{\text{1. Pfadregel}}}}{P(K)} \\[0.8em] &= \frac{0{,}35 \cdot 0{,}7}{0{,}8625} \\[0.8em] &\approx 0{,}2841 \\[0.8em] &= 28{,}41\,\% \end{align*}\]


