Schnittwinkel zwischen zwei Geraden
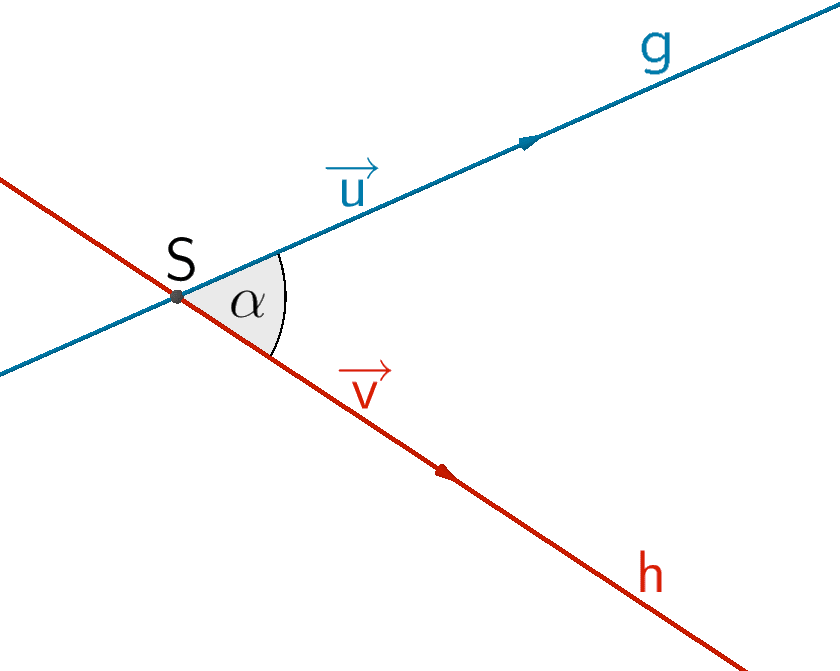
Unter dem Schnittwinkel zweier Geraden \(g \colon \overrightarrow{X} = \overrightarrow{A} + \lambda \cdot \overrightarrow{u}\,; \; \lambda \in \mathbb R\) und \(h \colon \overrightarrow{X} = \overrightarrow{B} + \mu \cdot \overrightarrow{v}\,; \; \mu \in \mathbb R\) versteht man den spitzen Winkel \(\alpha\), den die Richtungsvektoren \(\overrightarrow{u}\) und \(\overrightarrow{v}\) festlegen.
Schnittwinkel \(\boldsymbol{\alpha}\) zwischen zwei Geraden
\[\cos \alpha = \frac{\vert \overrightarrow{u} \circ \overrightarrow{v} \vert}{\vert \overrightarrow{u} \vert \cdot \vert \overrightarrow{v} \vert} \qquad (0^{\circ} \leq \alpha \leq 90^{\circ})\]
Je nach Aufgabenstellung ist vorab der Berechnung des Schnittwinkels zweier Geraden ggf. nachzuweisen, dass sich die Geraden schneiden (vgl. Abiturskript - 2.3.1 Lagebeziehung von Geraden).
Beispielaufgabe
Gegeben seien die Geraden \(g \colon \overrightarrow{X} = \begin{pmatrix} -4 \\ -1 \\ 4 \end{pmatrix} + \lambda \cdot \begin{pmatrix} 1 \\ -2 \\ 2 \end{pmatrix}; \; \lambda \in \mathbb R\) und \(h \colon \overrightarrow{X} = \begin{pmatrix} -9 \\ 9 \\ 2 \end{pmatrix} + \mu \cdot \begin{pmatrix} -1 \\ 2 \\ 2 \end{pmatrix}; \; \mu \in \mathbb R\).
Berechnen Sie den Schnittwinkel \(\alpha\) der Geraden \(g\) und \(h\).
\[g \colon \overrightarrow{X} = \begin{pmatrix} -4 \\ -1 \\ 4 \end{pmatrix} + \lambda \cdot \begin{pmatrix} 1 \\ -2 \\ 2 \end{pmatrix}; \; \lambda \in \mathbb R \quad \Longrightarrow \quad \overrightarrow{u} = \begin{pmatrix} 1 \\ -2 \\ 2 \end{pmatrix}\]
\[h \colon \overrightarrow{X} = \begin{pmatrix} -9 \\ 9 \\ 2 \end{pmatrix} + \mu \cdot \begin{pmatrix} -1 \\ 2 \\ 2 \end{pmatrix}; \; \mu \in \mathbb R \quad \Longrightarrow \quad \overrightarrow{v} = \begin{pmatrix} -1 \\ 2 \\ 2 \end{pmatrix}\]
\[\begin{align*}\cos \alpha &= \frac{\vert \overrightarrow{u} \circ \overrightarrow{v} \vert}{\vert \overrightarrow{u} \vert \cdot \vert \overrightarrow{v} \vert} \\[0.8em] &= \frac{\left|\begin{pmatrix} 1 \\ -2 \\ 2 \end{pmatrix} \circ \begin{pmatrix} -1 \\ 2 \\ 2 \end{pmatrix}\right|}{\left| \begin{pmatrix} 1 \\ -2 \\ 2 \end{pmatrix} \right| \cdot \left| \begin{pmatrix} -1 \\ 2 \\ 2 \end{pmatrix} \right|} \\[0.8em] &= \frac{\vert 1 \cdot (-1) + (-2) \cdot 2 + 2 \cdot 2 \vert}{\sqrt{1^{2} + (-2)^{2} + 2^{2}} \cdot \sqrt{(-1)^{2} + 2^{2} + 2^{2}}} \\[0.8em] &= \frac{\vert -1 \vert}{\sqrt{9} \cdot \sqrt{9}} \\[0.8em] &= \frac{1}{9} \qquad | \; \text{TR:} \; \cos^{-1}\left( \dfrac{1}{9}\right) \\[3.2em] &\alpha \approx 83{,}62^{\circ}\end{align*}\]


