Zeigen Sie, dass \(g_k(-x) = -g_{-k}(x)\) für alle \(x \in \mathbb R\) gilt, und interpretieren Sie diese Gleichung mit Blick auf die Graphen der Funktionen \(g_k\) und \(g_{-k}\).
(4 BE)
Lösung zu Teilaufgabe 2b
\[g_k(x) = -5x \cdot e^{-kx}; \; D_{g_k} = \mathbb R, \; k \in \mathbb R \backslash \{0\}\]
Nachweis, dass \(g_k(-x) = -g_{-k}(x)\) für alle \(x \in \mathbb R\) gilt
\[\begin{align*}g_k(-x) &= -5 \cdot (-x) \cdot e^{-k \cdot (-x)} \\[0.8em] &= \textcolor{#cc071e}{-}\left( -5x \cdot e^{-(\textcolor{#cc071e}{-k}) \cdot x}\right) \\[0.8em] &= \textcolor{#cc071e}{-}g_{\textcolor{#cc071e}{-k}}(x)\end{align*}\]
Interpretation der Gleichung \(g_k(-x) = -g_{-k}(x)\)
Die Graphen der Funktionen \(g_k\) und \(g_{-k}\) sind punktsymmetrisch bezüglich des Koordinatenursprungs.
Symmetrie von Funktionsgraphen bzgl. des Koordinatensystems
Der Graph einer Funktion \(f\) ist
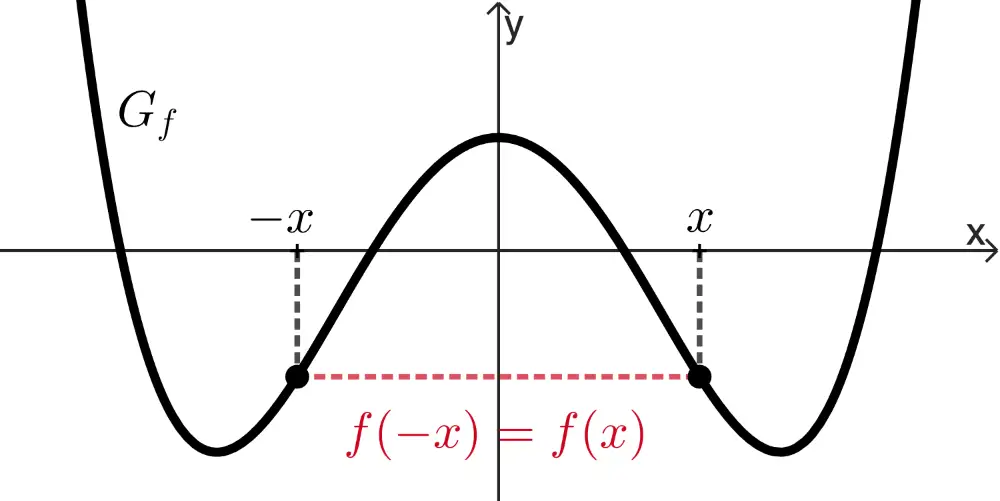
achsensymmetrisch bzgl. der \(\boldsymbol{y}\)-Achse,
wenn für alle \(x \in D_f\) gilt: \(f(-x) = f(x)\).
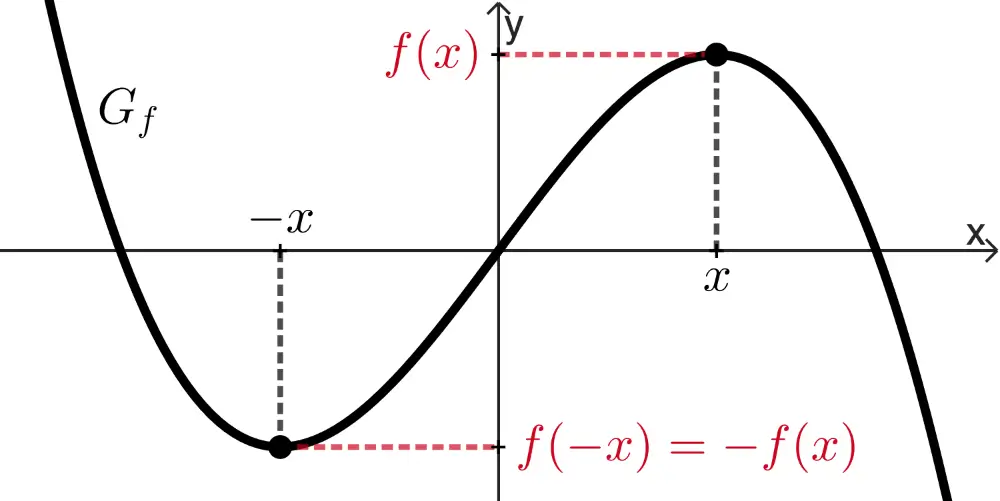
punktsymmetrisch bzgl. des Koordinatenursprungs,
wenn für alle \(x \in D_f\) gilt: \(f(-x) = -f(x)\)
Ergänzende Erklärung (nicht verlangt)
Der Graph einer Funktion \(f\) ist punktsymmetrisch bezüglich des Koordinatenursprung, wenn \(f(-x) = -f(x)\) gilt.
Die Graphen zweier Funktionen \(f\) und \(g\) sind punktsymmetrisch bezüglich des Koordinatenursprung, wenn \(f(-x) =-g(x)\) gilt.
Die Graphen der Funktionen \(g_k\) und \(g_{-k}\) sind punktsymmetrisch bezüglich des Koordinatenursprungs, da \(g_k(-x) = -g_{-k}(x)\) gilt.


