Abbildung 2 zeigt den Graphen einer in \(\mathbb R\) definierten differenziebaren Funktion \(g \colon x \mapsto g(x)\). Mithilfe des Newton-Verfahrens soll ein Näherungswert für die Nullstelle \(a\) von \(g\) ermittelt werden. Begründen Sie, dass weder die \(x\)-Koordinate des Hochpunkts \(H\) noch die \(x\)-Koordinate des Tiefpunkts \(T\) als Startwert des Newton-Verfahrens gewählt werden kann.
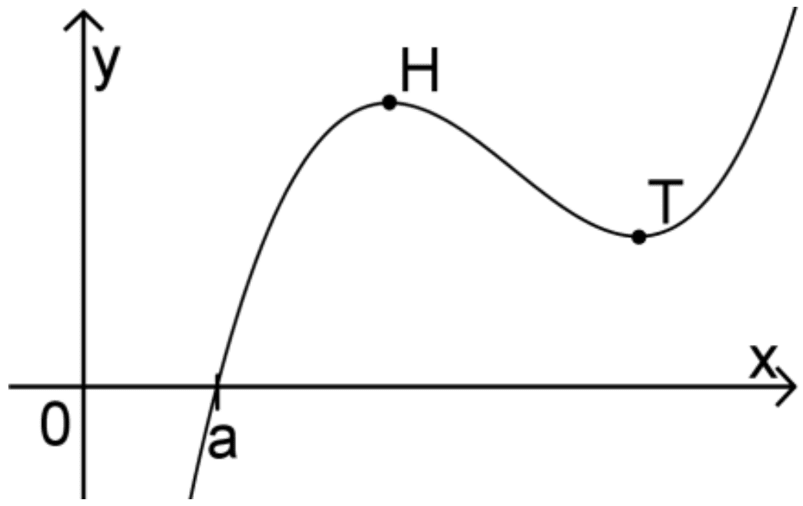Abb. 2
(2 BE)
Lösung zu Teilaufgabe 4
Newton-Verfahren
Newton-Verfahren
\(x_{n + 1} = x_n - \dfrac{f(x_n)}{f'(x_n)}\) mit \(n \in \mathbb N\) und \(f'(x_n) \neq 0\)
(vgl. Merkhilfe)
Begründung mithilfe der Newtonschen Iterationsformel:
\[x_{n + 1} = x_{0} - \frac{g(x_{0})}{g'(x_{0})}\,; \enspace g'(x_{0}) \neq 0\]
Wegen \(g'(x_{H}) = 0\) bzw. \(g'(x_{T}) = 0\) kann weder die \(x\)-Koordinate des Hochpunkts \(H\) noch die \(x\)-Koordinate des Tiefpunkts \(T\) als Startwert gewählt werden.
Graphische Begründung:
Das Newton-Verfahren errechnet einen Näherungswert für die Nullstelle einer Funktion, indem es die Nullstelle (Schnittstelle mit der \(x\)-Achse) der Tangente an die Funktion an der Stelle \(x_{0}\) (Startwert) ermittelt. Da die Tangente an eine Funktion an den Extremstellen waagrecht (parallel zur \(x\)-Achse) verläuft, existiert keine Nullstelle der Tangente und somit auch kein Näherungswert.
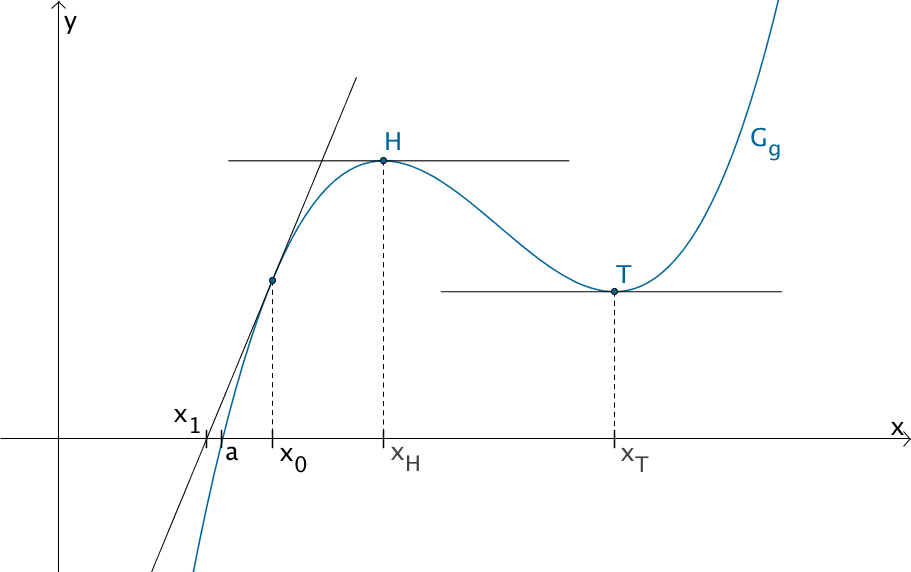
Newton-Verfahren: Die Tangente an den Graphen der Funktion \(g\) an der Stelle \(x_{0}\) (Startwert) schneidet die \(x\)-Achse an der Stelle \(x_{1}\), einem ersten Näherungswert für die Nullstelle \(a\) der Funktion \(g\). Die Extremstellen \(x_{H}\) und \(x_{T}\) können nicht als Startwert gewählt werden, da die Tangenten an \(G_{g}\) an den Extremstellen waagrecht verlaufen und folglich die \(x\)-Achse nicht schneiden.
