Um Geld für die Ausstattung des örtlichen Kindergartens einzunehmen, veranstaltet der Supermarkt ein Gewinnspiel. Die fünf Sektoren des dabei eingesetzten Glücksrads sind von 1 bis 5 durchnummeriert. Die Größe der Sektoren ist direkt proportional zum Zahlenwert der Nummern; beispielsweise ist der Sektor mit der Nummer 3 dreimal so groß wie der Sektor mit der Nummer 1. Nachdem der Spieler sechs Euro bezahlt hat, wird das Glücksrad einmal gedreht. Erzielt der Spieler eine der Nummern 1 bis 4, so wird ihm der zugehörige Zahlenwert als Betrag in Euro ausgezahlt, erzielt er die Nummer 5, so erhält er eine Eintrittskarte für einen Freizeitpark im Wert von fünfzehn Euro.
Bestimmen Sie die Größe des Öffnungswinkels des Sektors mit der Nummer 1 sowie die Wahrscheinlichkeit dafür, dass ein Spieler bei einem Spiel eine Eintrittskarte gewinnt
(Teilergebnis: Größe des Öffnungswinkels: 24°)
(3 BE)
Lösung zu Teilaufgabe 2a
Größe des Öffnungswinkels des Sektors mit der Nummer 1
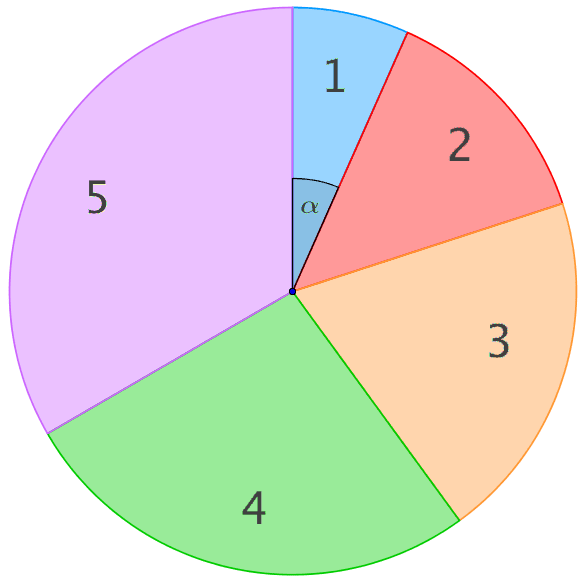
Beispiel für ein Glücksrad mit den Sektoren 1 bis 5
Es sei \(\alpha\) das Maß des Öffnungswinkel des Sektors mit der Nummer 1.
\[\begin{align*}\alpha + 2 \cdot \alpha + 3 \cdot \alpha + 4 \cdot \alpha + 5 \cdot \alpha &= 360^{\circ} \\[0.8em] 15\alpha &= 360^{\circ} & &| : 15 \\[0.8em] \alpha &= \frac{360^{\circ}}{15} \\[0.8em] \alpha &= 24^{\circ}\end{align*}\]
Wahrscheinlichkeit dafür, dass ein Spieler beim einem Spiel eine Eintrittskarte gewinnt
Der Öffnungswinkel des Sektors mit der Nummer 5 beträgt \(5 \cdot 24^{\circ} = 120^{\circ}\).
\[P(\text{„Eintrittskarte"}) = P(\text{„Nummer 5"}) = \frac{120^{\circ}}{360^{\circ}} = \frac{1}{3}\]


