Begründen Sie, dass die Dreiecke \(BCM\) und \(ABM\) den gleichen Flächeninhalt besitzen, ohne diesen zu berechnen.
(2 BE)
Lösung zu Teilaufgabe 1b
1. Möglichkeit: Seitenhalbierende
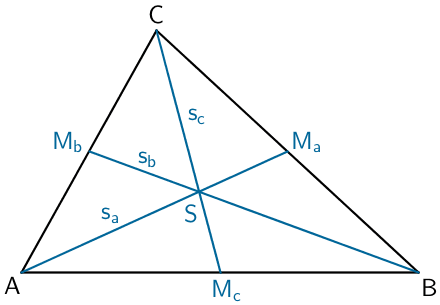
Besondere Linien und Punkte eines Dreiecks:
Seitenhalbierende
Die Seitenhalbierenden eines Dreiecks verbinden jeweils den Mittelpunkt einer Seite mit dem gegenüberliegenden Eckpunkt. Sie schneiden sich im Schwerpunkt des Dreiecks.
Der Schwerpunkt teilt die Seitenhalbierenden im Verhältnis 2 : 1.
Die Seitenhalbierenden teilen ein Dreieck jeweils in zwei flächengleiche Dreiecke.
![Seitenhalbierende [BM] des Dreiecks ABC](/images/stories/B2019_PT_A_G1/B2019_PT_A_G1_1b.png)
Die Seitenhalbierende \(\textcolor{#cc071e}{[BM]}\) teilt das Dreieck \(ABC\) in die beiden flächeninhaltsgleichen Dreiecke \(ADM\) und \(BCM\).
2. Möglichkeit: Flächeninhalt eines Dreiecks
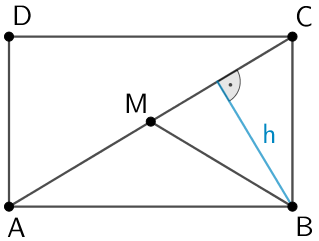
Höhe \(\textcolor{#0087c1}{h}\) der Dreiecke \(ABM\) und \(BCM\)
Es gilt: \(A_{ABM} = \frac{1}{2} \cdot \overline{AM} \cdot \textcolor{#0087c1}{h}\) und \(A_{BCM} = \frac{1}{2} \cdot \overline{CM} \cdot \textcolor{#0087c1}{h}\)
Mit \(\overline{AM} = \overline{CM}\) folgt: \(A_{ABM} = A_{BCM}\)


