Die Abbildung zeigt den Würfel \(ABCDEFG\) mit \(A(0|0|0)\) und \(G(5|5|5)\) in einem kartesischen Koordinatensystem. Die Ebene \(T\) schneidet die Kanten des Würfels unter anderem in den Punkten \(I(5|0|1)\), \(J(2|5|0)\), \(K(0|5|2)\) und \(L(1|0|5)\).
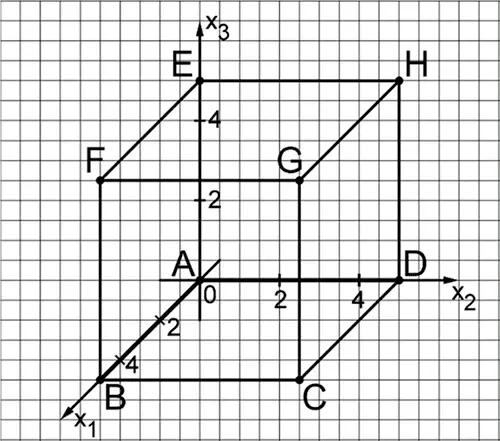
Zeichnen Sie das Viereck \(IJKL\) in die Abbildung ein und zeigen Sie, dass es sich um ein Trapez handelt, bei dem zwei gegenüberliegende Seiten gleich lang sind.
(4 BE)
Lösung zu Teilaufgabe a
Einzeichnen des Vierecks \(IJKL\)
\(I(5|0|1)\), \(J(2|5|0)\), \(K(0|5|2)\), \(L(1|0|5)\)
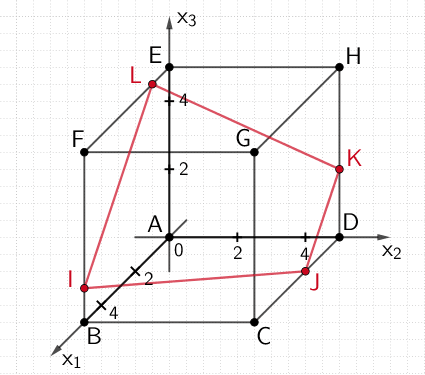
Viereck \(\textcolor{#cc071e}{IJKL}\)
Nachweis, dass das Viereck \(IJKL\) ein Trapez mit zwei gleichlangen gegenüberliegenden Seiten ist
Anhand der Zeichnung des Vierecks \(IJKL\) ist zu erkennen, dass die Seiten \([JK]\) und \([IL]\) die zueinander parallelen Grundlinien des Trapezes sind, und dass die Seiten \([IJ]\) und \([KL]\) die gleichlangen gegenüberliegenden Seiten sein müssen. Somit ist nachzuweisen, dass \(\overrightarrow{JK} \parallel \overrightarrow{IL}\) und \(\overline{IJ} = \overline{KL}\) gilt.
\(I(5|0|1)\), \(J(2|5|0)\), \(K(0|5|2)\), \(L(1|0|5)\)
\[\overrightarrow{JK} = \overrightarrow{K} - \overrightarrow{J} = \begin{pmatrix} 0 \\ 5 \\ 2 \end{pmatrix} - \begin{pmatrix} 2 \\ 5 \\ 0 \end{pmatrix} = \begin{pmatrix} -2 \\ 0 \\ 2 \end{pmatrix}\]
\[\overrightarrow{IL} = \overrightarrow{L} - \overrightarrow{I} = \begin{pmatrix} 1 \\ 0 \\ 5 \end{pmatrix} - \begin{pmatrix} 5 \\ 0 \\ 1 \end{pmatrix} = \begin{pmatrix} -4 \\ 0 \\ 4 \end{pmatrix}\]
Lineare (Un-)Abhängigkeit von zwei Vektoren
Zwei Vektoren \(\overrightarrow{a}\) und \(\overrightarrow{b}\) sind
linear abhängig, wenn
\(\overrightarrow{a} \parallel \overrightarrow{b}\quad\) bzw. \(\quad\overrightarrow{a} = k \cdot \overrightarrow{b}\,; \enspace k \in \mathbb R \quad\) gilt.
linear unabhängig, wenn
\(\overrightarrow{a} \nparallel \overrightarrow{b}\quad\) bzw. \(\quad\overrightarrow{a} \neq k \cdot \overrightarrow{b}\,; \enspace k \in \mathbb R \quad\) gilt.
Lineare (Un-)Abhängigkeit von drei Vektoren
Drei Vektoren \(\overrightarrow{a}\), \(\overrightarrow{b}\) und \(\overrightarrow{c}\) sind
linear abhängig, wenn
sie in einer Ebene liegen bzw. wenn
die lineare Vektorgleichung \(\overrightarrow{c} = r \cdot \overrightarrow{a} + s \cdot \overrightarrow{b}\) eine eindeutige Lösung hat.
linear unabhängig, wenn
sie den Raum \(\mathbb R^{3}\) aufspannen bzw. wenn
die lineare Vektorgleichung \(\overrightarrow{c} = r \cdot \overrightarrow{a} + s \cdot \overrightarrow{b}\) keine Lösung hat.
Bei der Untersuchung der linearen (Un)Abhängigkeit dreier Vektoren spielt es keine Rolle, welche der drei Vektoren \(\overrightarrow{a}\), \(\overrightarrow{b}\) oder \(\overrightarrow{c}\) man als Linearkombination der beiden anderen Vektoren darzustellen versucht.
\[\Longrightarrow \quad \overrightarrow{IL} = 2 \cdot \overrightarrow{JK} \quad \Longrightarrow \quad \overrightarrow{IL} \parallel \overrightarrow{JK}\]
Also sind die Seiten \([JK]\) und \([IL]\) zueinander parallel.
Betrag eines Vektors
\[ \vert \overrightarrow{a} \vert = \sqrt{\overrightarrow{a} \circ \overrightarrow{a}} = \sqrt{{a_1}^2 + {a_2}^2 + {a_3}^2}\]
(vgl. Merkhilfe)
\[\begin{align*} \overline{IJ} &= \vert \overrightarrow{IJ} \vert = \vert \overrightarrow{J} - \overrightarrow{I} \vert \\[0.8em] &= \left| \begin{pmatrix} 2 \\ 5 \\ 0 \end{pmatrix} - \begin{pmatrix} 5 \\ 0 \\ 1 \end{pmatrix} \right| = \left| \begin{pmatrix} -3 \\ 5 \\ -1 \end{pmatrix} \right| \\[0.8em] &= \sqrt{(-3)^{2} + 5^{2} + (-1)^{2}} = \sqrt{35} \end{align*}\]
\[\begin{align*} \overline{KL} &= \vert \overrightarrow{KL} \vert = \vert \overrightarrow{L} - \overrightarrow{K} \vert \\[0.8em] &= \left| \begin{pmatrix} 1 \\ 0 \\ 5 \end{pmatrix} - \begin{pmatrix} 0 \\ 5 \\ 2 \end{pmatrix} \right| = \left| \begin{pmatrix} 1 \\ -5 \\ 3 \end{pmatrix} \right| \\[0.8em] &= \sqrt{1^{2} + (-5)^{2} + 3^{2}} = \sqrt{35} \end{align*}\]
Also sind die Seiten \([IJ]\) und \([KL]\) gleichlang.
Das Viereck \(IJKL\) ist somit ein Trapez mit zwei gegenüberliegenden gleichlangen Seiten (gleichschenkliges Trapez).


