Für einen anderen Tag wird die momentane Änderungsrate der Staulänge für den Zeitraum von 06:00 Uhr bis 10:00 Uhr durch den in der Abbildung 2 gezeigten Graphen dargestellt. Dabei ist \(x\) die nach 06:00 Uhr vergangene Zeit in Stunden und \(y\) die momentane Änderungsrate der Staulänge in Kilometer pro Stunde.
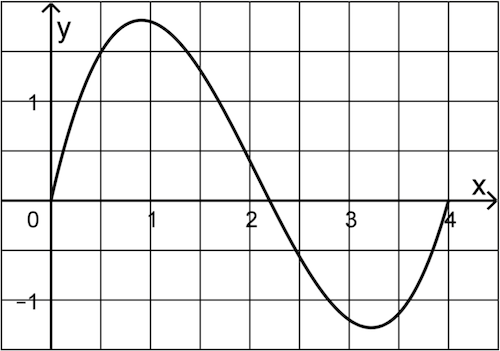Abb. 2
Um 07:30 Uhr hat der Stau eine bestimmte Länge. Es gibt einen anderen Zeitpunkt, zu dem der Stau die gleiche Länge hat. Markieren Sie diesen Zeitpunkt in der Abbildung 2, begründen Sie Ihre Markierung und veranschaulichen Sie Ihre Begründung in der Abbildung 2.
(3 BE)
Lösung zu Teilaufgabe 1g
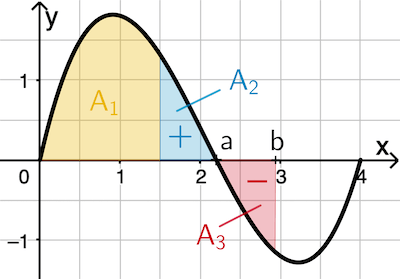Abb. 2
Zum Zeitpunkt \(b \approx 2{,}9\) hat der Stau die gleiche Länge wie um 07:30 Uhr.
Mögliche Begründung
Der Flächeninhalt \(\textcolor{#e9b509}{A_1}\) entspricht der Staulänge um 07:30 Uhr (\(x = 1{,}5\)). Nach 07:30 Uhr nimmt die Staulänge weiter zu, bis der Zeitpunkt \(a \approx 2{,}2\) erreicht ist. Diese Zunahme entspricht dem Flächeninhalt \(\textcolor{#0087c1}{A_2}\). Im Zeitraum \([a;b]\) nimmt die Staulänge gleichermaßen wieder ab \((\textcolor{#0087c1}{A_2} = \textcolor{#cc071e}{A_3})\), sodass die Stelle \(b\) den Zeitpunkt markiert, zu dem der Stau die gleiche Länge wie um 07:30 Uhr hat.
Ergänzende Erklärung (nicht verlangt)
Die Aufgabe behandelt in geometrischer Interpretation eine wichtige Anwendung der Integralrechnung.
Beschreibt eine Funktion \(f\) die momentane Änderungsrate einer Größe in Abhängigkeit von der Zeit \(t\), so errechnet das bestimmte Integral \(\displaystyle \int_{t_{1}}^{t_{2}}f(t)dt\) den Wert der Gesamtänderung der Größe im Zeitintervall \([t_{1};t_{2}]\).
Der Verlauf des Graphen in Abbildung 2 beschreibt die momentane Änderungsrate der Staulänge.
In obiger Begründung vertreten die Flächeninhalte \(\textcolor{#e9b509}{A_1}\), \(\textcolor{#0087c1}{A_2}\) und \(\textcolor{#cc071e}{A_3}\) in geometrischer Interpretation die Werte der bestimmten Integrale, mit denen sich die Gesamtänderung der Staulänge im jeweiligen Zeitintervall berechnen ließe, wenn die zum Graphen in Abbildung 2 gehörende Funktion bekannt wäre.
