Berechnen Sie mithilfe der Funktion \(q\) einen Näherungswert für den Flächeninhalt \(A\) des vom Kunstwerk eingenommenen Teils der Wand.
(4 BE)
Lösung zu Teilaufgabe 1e
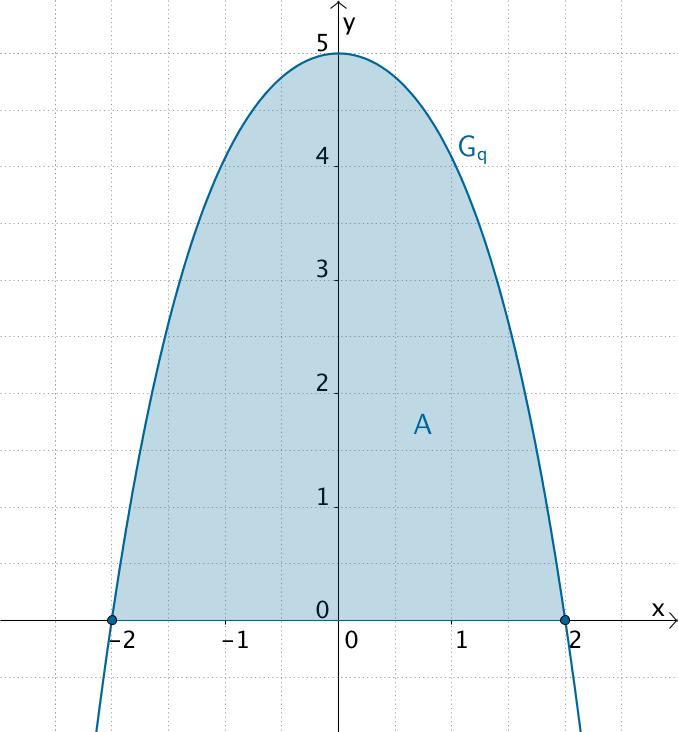
Der Flächeninhalt \(\,A\,\) des vom Kunstwerk eingenommenen Teils der Wand entspricht näherungsweise dem Flächeninhalt des Flächenstücks, das der Graph von \(\,q\,\) mit der \(\,x\)-Achse einschließt. Der Flächninhalt ist ein Näherungswert, weil die Funktion \(q\) den Rand des Kunstwerks nicht exakt beschreibt, sondern nur annähert (siehe Teilaufgabe 1b).
\[q(x) = -0{,}11x^4 - 0{,}81x^2 + 5\,; \quad D_q = \mathbb R\]
\[A = \int_{-2}^2 q(x)\,dx\]
Berechnung bestimmter Integrale
\[\int_{a}^{b} f(x)\,dx = [F(x)]_{a}^{b} = F(b) - F(a)\]
Dabei ist \(F\) eine beliebige Stammfunktion zu \(f\).
(vgl. Merkhilfe)
Eigenschaften des bestimmten Integrals - Integrationsregeln
Identische Integrationsgrenzen:
\[\int_{a}^{a} f(x)\,dx = 0\]
Faktorregel:
\(\displaystyle \int_{a}^{b} c \cdot f(x)\,dx = c \cdot \int_{a}^{b} f(x)\,dx\) mit \(c \in \mathbb R\)
Summenregel:
\[\int_{a}^{b} \left[f(x) \pm g(x) \right] dx = \int_{a}^{b}f(x)\,dx \pm \int_{a}^{b}g(x)\,dx\]
Vertauschungsregel:
\[\int_{a}^{b}f(x)\,dx = -\int_{b}^{a}f(x)\,dx\]
Zerlegung in Teilintervalle:
\(\displaystyle \int_{a}^{b}f(x)\,dx = \int_{a}^{c}f(x)\,dx + \int_{c}^{b}f(x)\,dx\) mit \(a \leq c \leq b\)
Stammfunktion \(Q\) bestimmen:
Stammfunktion einer Potenzfunktion
\[f(x) = x^r \quad \Longrightarrow \quad F(x) = \frac{1}{r + 1} \cdot x^{r + 1} + C\]
\[r \neq -1\]
\[\begin{align*} Q(x) &= -0{,}11 \cdot \frac{1}{5}x^5 - 0{,}81 \cdot \frac{1}{3}x^3 + 5x + C \\[0.8em] &= -0{,}022x^5 - 0{,}27x^3 + 5x + C \end{align*}\]
Flächeninhalt \(A\) berechnen:
\[\begin{align*}A &= \big[ -0{,}022x^5 - 0{,}27x^3 + 5x \, \big]_{-2}^2 \\[0.8em] &= -0{,}022 \cdot 2^5 - 0{,}27 \cdot 2^3 + 5 \cdot 2 - \big( -0{,}022 \cdot (-2)^5 - 0{,}27 \cdot (-2)^3 + 5 \cdot (-2) \big) \\[0.8em] &\approx 14{,}3 \end{align*}\]
Der Flächeninhalt \(A\) des vom Kunstwerk eingenommenen Teils der Wand beträgt näherungsweise 14,3 m².


