Die Gerade mit der Gleichung \(y = x - 1\) begrenzt gemeinsam mit den Koordinatenachsen ein Dreieck. Geben Sie den Flächeninhalt dieses Dreiecks und den sich daraus ergebenden Näherungswert für \(F(1)\) an.

(2 BE)

Lösung zu Teilaufgabe 2b

 

Flächeninhalt des Dreiecks: \(A_{\triangle} = 0{,}5 \,\sf{FE}\)

Näherungswert für \(F(1)\): \(F(1) \approx -0{,}5\)

 

Begründung (nicht verlangt)

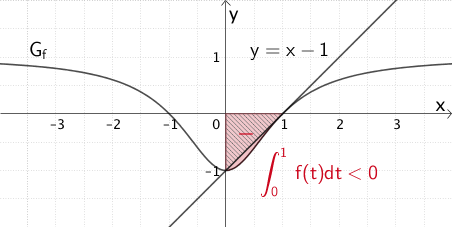
Gerade mit der Gleichung y = x - 1, Flächenstück, welches der Graph von f im Bereich 0 ≤ x ≤ 1 mit der x-Achse einschließt

Die Gerade mit der Gleichung \(y = x - 1\) schneidet die \(x\)-Achse an der Stelle \(x = 1\) (Nullstelle) und die \(y\)-Achse bei \(y = -1\) (\(y\)-Achsenabschnitt). Der Flächeninhalt des Dreiecks, das die Gerade mit den Koordinatenachsen begrenzt, ergibt sich folglich zu:

 

\[A_{\triangle} = \frac{1}{2} \cdot 1 \cdot 1 = 0{,}5\,\sf{FE}\]

 

Der Flächeninhalt des Dreiecks entspricht näherungsweise dem Flächeninhalt des Flächenstücks, welches \(G_{f}\) im Bereich \(0 \leq x \leq 1\) mit der \(x\)-Achse einschließt.

Das bestimmte Integral \(\displaystyle \int_{0}^{1}f(1)dt\) errechnet die Maßzahl des Flächeninhalts dieses Flächenstücks. Da \(G_{f}\) im Bereich \(0 \leq x \leq 1\) unterhalb der \(x\)-Achse verläuft, gilt:

 

\[\textcolor{#cc071e}{\int_{0}^{1}f(t)dt < 0}\]

 

Somit folgt für den Näherungswert von \(F(1)\):

 

\[F(1) = \textcolor{#cc071e}{\underbrace{\int_{0}^{1}f(t)dt}_{<\,0}} \approx \textcolor{#cc07e1}{\mathbf{-}}(\underbrace{\frac{1}{2} \cdot 1 \cdot 1}_{A_{\triangle}}) = -0{,}5\]