Beschreiben Sie, wie man mithilfe der Abbildung für eine Fahrt mit einer Gesamtfahrzeit zwischen zwei und vierzehn Stunden die zugehörige Eigengeschwindigkeit des Boots näherungsweise ermitteln kann. Berechnen Sie auf der Grundlage des Modells die Eigengeschwindigkeit des Boots für eine Fahrt mit einer Gesamtfahrzeit von vier Stunden.
(5 BE)
Lösung zu Teilaufgabe 2e
Näherungsweise grafische Ermittlung der Eigengeschwindigkeit für \(2 < t(x) < 14\)
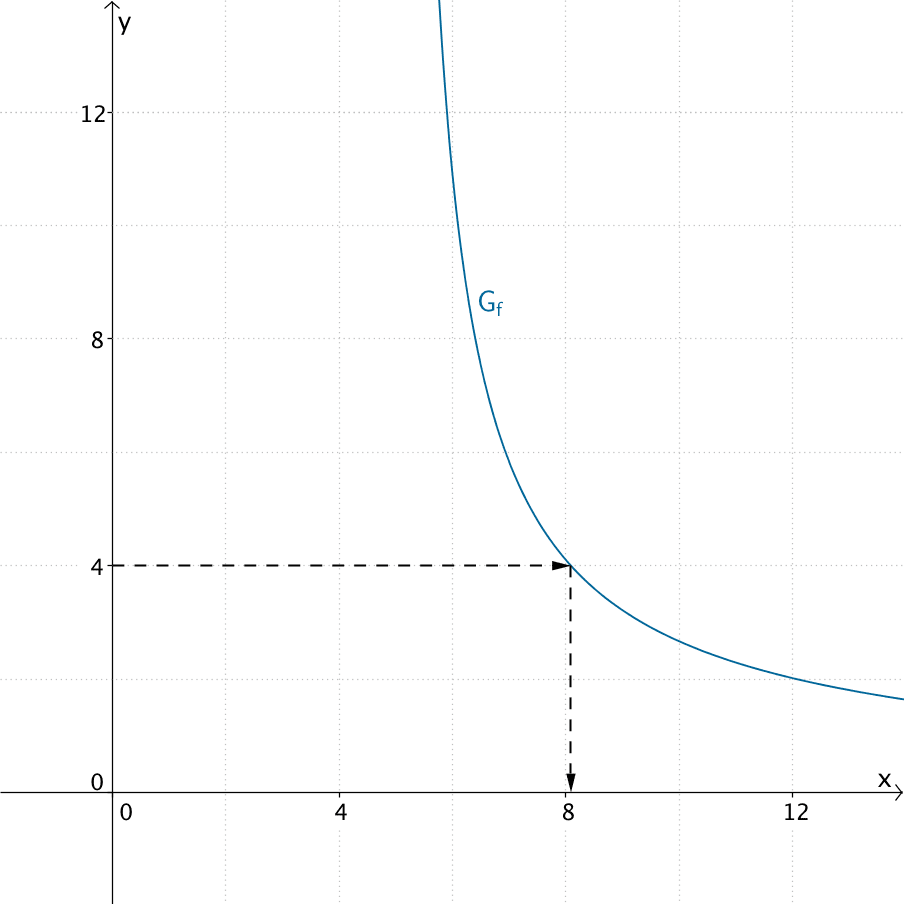
Die zu Beginn der Aufgabengruppe 2 gegebene Abbildung zeigt den Graphen der Funktion \(f\) für \(5 < x < 14\). Wegen \(f(x) \Longleftrightarrow t(x)\) (siehe Teilaufgabe 2d) kann \(G_{f}\) für eine grafische Lösung nach dem Modell aus Teilaufgabe 2 verwendet werden, um für eine Fahrt mit einer Gesamtfahrzeit zwischen zwei und vierzehn Stunden die zugehörige Eigengeschwindigkeit des Bootes näherungsweise zu ermitteln..
Dabei gibt die \(y\)-Koordinate eines Graphenpunktes von \(G_f\) die Gesamtfahrzeit in Stunden an und die \(x\)-Koordinate die zugehörige Eigengeschwindigkeit des Bootes in \(\frac{\sf{km}}{\sf{h}}\). So liest man beispielsweise für eine Gesamtfahrzeit von vier Stunden näherungsweise eine Eigengeschwindigkeit des Bootes von \(8\frac{\sf{km}}{\sf{h}}\) ab.
Eigengeschwindigkeit des Bootes nach dem Modell für eine Fahrt mit einer Gesamtfahrzeit von vier Stunden
\[t(x) = \frac{10}{x + 5} + \frac{10}{x - 5}\,; \quad x > 5\]
\[f(x) = \frac{20x}{x^2 - 25}\]
\[\begin{align*}t(x) &= 4 \\[0.8em] \frac{10}{x + 5} + \frac{10}{x - 5} &= 4 & &| \; t(x) \Longleftrightarrow f(x) \\[0.8em] \frac{20x}{x^2 - 25} &= 4 & &| \cdot (x^2 - 25) \\[0.8em] 20x &= 4 \cdot(x^2 - 25) \\[0.8em] 20x &= 4x^2 - 100 & &| - 20x \\[0.8em] 0 &= 4x^2 - 20x - 100 \end{align*}\]
Lösungsformel für quadratische Gleichungen (vgl. Merkhilfe)
\[ax^2 + bx + c = 0 \,, \qquad a, b, c \in \mathbb R \,, \quad a \neq 0\]
\[\begin{align*} x_{1,2} &= \frac{-b \pm \sqrt{b^2 - 4ac}}{2a}, \quad b^2 \geq 4ac \\[0.8em] x_{1,2} &= \frac{-b \pm \sqrt{D}}{2a}, \quad D \geq 0 \end{align*}\]
Diskriminante \(D = b^2 -4ac \;\):
\(D < 0\,\): keine Lösung
\(D = 0\,\): genau eine Lösung
\(D > 0\,\): zwei verschiedene Lösungen
\[\begin{align*}x_{1,2} &= \frac{20 \pm \sqrt{(-20)^2 - 4 \cdot 4 \cdot (-100)}}{2 \cdot 4} \\[0.8em] &= \frac{20 \pm \sqrt{2000}}{8} \\[0.8em] &= \frac{20 \pm 20\sqrt{5}}{8} \\[0.8em] &= \frac{5 \pm 5\sqrt{5}}{2} \\[0.8em]\end{align*}\]
\[x_{1} = \frac{5 + 5\sqrt{5}}{2} \approx 8{,}09\]
\[\left(x_{2} = \frac{5 - 5\sqrt{5}}{2} \approx -3{,}09\right)\]
Für eine Gesamtfahrzeit von vier Stunden muss die Eigengeschwindigkeit des Bootes nach dem Modell ca. \(8{,}09\frac{\sf{km}}{h}\) betragen.
Anmerkung: Die Lösung \(x_2 \approx -3{,}09\) liegt außerhalb des Definitionsbereichs \(D_{f} = ]5;\infty[\). Auch kommt sie im Sachzusammenhang nicht in Frage, da das Boot mit einer Eigengeschwindigkeit \(x > 5\) immer vorwärts fährt.


