Die Zufallsgröße \(Y\) kann die Werte 0, 1, 2, 3 und 4 annehmen. Die Tabelle zeigt die Wahrscheinlichkeitsverteilung von \(Y\) mit \(a, b \in [0;1]\).
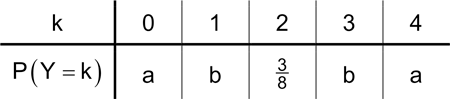
Beschreiben Sie, woran man unmittelbar erkennen kann, dass der Erwartungswert von \(Y\) gleich 2 ist.
(2 BE)
Lösung zu Teilaufgabe 3a
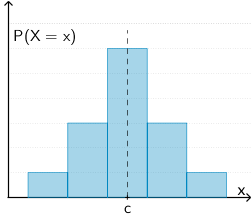
Ist die Wahrscheinlichkeitsverteilung einer Zufallsgröße \(X\) symmetrisch zu \(x = c\), so ist \(\mu = E(X) = c\) der Erwartungswert der Zufallsgröße.

Die Tabelle zeigt, dass die Werte \(k\) der Zufallsgröße \(Y\) symmetrisch um den Wert \(k = 2\) verteilt sind.
Zudem sind die Wahrscheinlichkeiten \(P(Y = k)\) symmetrisch um die Wahrscheinlichkeit \(P(Y = 2)\) verteilt.
Folglich ist \(\mu = E(Y) = 2\) der Erwartungswert der Zufallsgröße \(Y\).
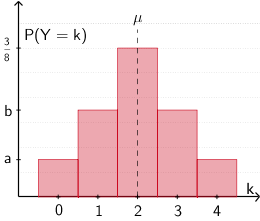
Histogramm einer möglichen Wahrscheinlichkeitsverteilung der Zufallsgröße \(Y\) (nicht verlangt)

