Die Abbildung zeigt modellhaft ein Einfamilienhaus, das auf einer horizontalen Fläche steht. Auf einer der beiden rechteckigen Dachflächen soll eine Dachgaube errichtet werden. Die Punkte \(A\), \(B\), \(C\), \(D\), \(O\), \(P\), \(Q\) und \(R\) sind die Eckpunkte eines Quaders. Das gerade dreiseitige Prisma \(LMNIJK\) stellt die Dachgaube dar, die Strecke \([GH]\) den First des Dachs, d.h. die obere waagrechte Dachkante. Eine Längeneinheit im Koordinatensystem entspricht 1 m, d.h. das Haus ist 10 m lang.
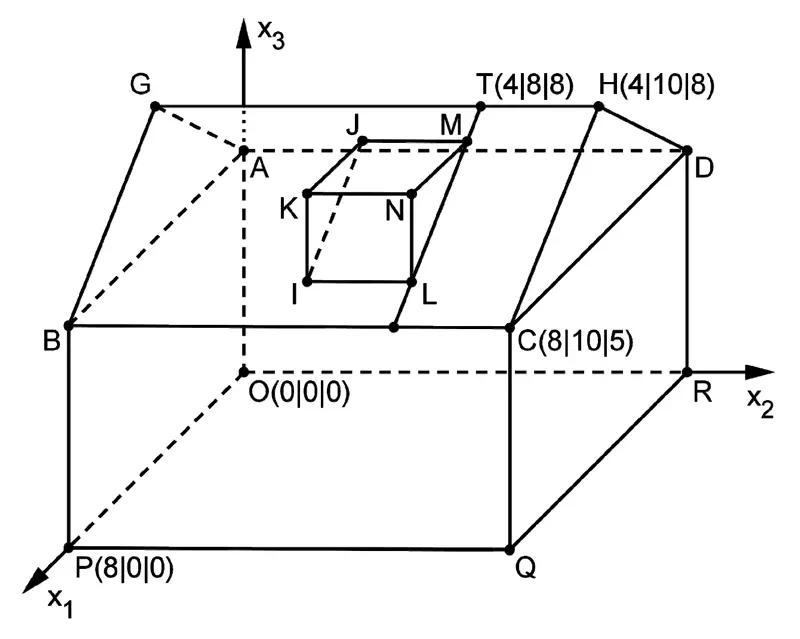
Berechnen Sie den Inhalt derjenigen Dachfläche, die im Modell durch das Rechteck \(BCHG\) dargestellt wird.
(2 BE)
Lösung zu Teilaufgabe a
Die Eckpunkte des Rechtecks \(BCHG\) können der Zeichnung entnommen werden.
\(B\,(8|0|5)\), \(C\,(8|10|5)\), \(H\,(4|10|8)\), \(G\,(4|0|8)\)
1. Lösungsansatz: Elementargeometrischer Ansatz
Betrag eines Vektors
\[ \vert \overrightarrow{a} \vert = \sqrt{\overrightarrow{a} \circ \overrightarrow{a}} = \sqrt{{a_1}^2 + {a_2}^2 + {a_3}^2}\]
(vgl. Merkhilfe)
\[\begin{align*} A_{BCHG} &= \vert \overrightarrow{CB} \vert \cdot \vert \overrightarrow{CH} \vert \\[0.8em] &= \vert \overrightarrow{B} - \overrightarrow{C} \vert \cdot \vert \overrightarrow{H} - \overrightarrow{C} \vert \\[0.8em] &= \left| \begin{pmatrix} 8 \\ 0 \\ 5 \end{pmatrix} - \begin{pmatrix} 8 \\ 10 \\ 5 \end{pmatrix} \right| \cdot \left| \begin{pmatrix} 4 \\ 10 \\ 8 \end{pmatrix} - \begin{pmatrix} 8 \\ 10 \\ 5 \end{pmatrix} \right| \\[0.8em] &= \left| \begin{pmatrix} 0 \\ -10 \\ 0 \end{pmatrix} \right| \cdot \left| \begin{pmatrix} -4 \\ 0 \\ 3 \end{pmatrix} \right| \\[0.8em] &= \sqrt{0^2 + (-10)^2 + 0^2} \cdot \sqrt{(-4)^2 + 0^2 + 3^2} \\[0.8em] &= \sqrt{100} \cdot \sqrt{25} \\[0.8em] &= 10 \cdot 5 \\[0.8em] &= 50 \end{align*}\]
Der Flächeninhalt der Dachfläche, die im Modell durch das Rechteck \(BCHG\) dargestellt wird, beträgt 50 m2.
2. Lösungsansatz: Vektorprodukt anwenden
Anwendung des Vekorprodukts
Der Betrag des Vektorprodukts \(\overrightarrow{a} \times \overrightarrow{b}\) entspricht der Maßzahl des Flächeninhalts eines von zwei Vektoren \(\overrightarrow{a} \neq \overrightarrow{0}\) und \(\overrightarrow{b} \neq \overrightarrow{0}\) aufgespannten Parallelogramms.
\[\vert \overrightarrow{a} \times \overrightarrow{b} \vert = \vert \overrightarrow{a} \vert \cdot \textcolor{#cc071e}{\vert \overrightarrow{b} \vert \cdot \sin{\varphi}}\]
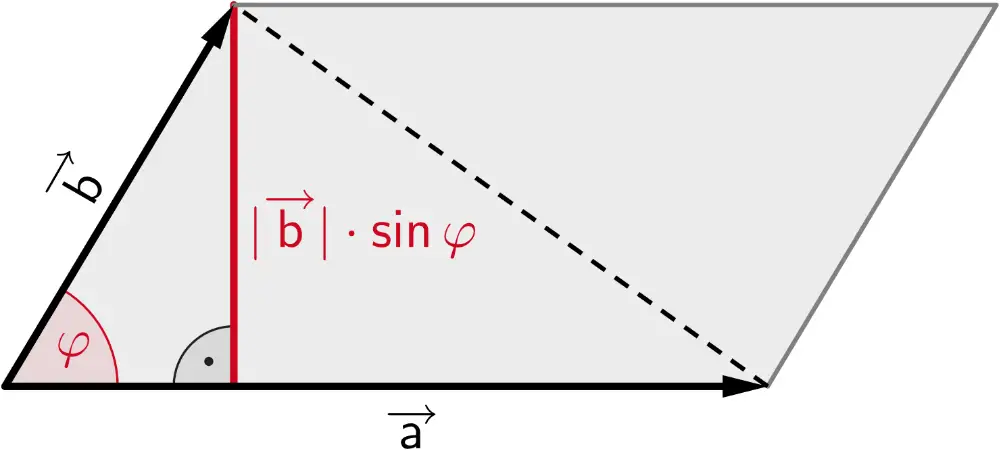
Flächeninhalt eines Parallelogramms
\[A = \vert \overrightarrow{a} \times \overrightarrow{b} \vert\]
Flächeninhalt eines Dreiecks
\[A = \frac{1}{2} \cdot \vert \overrightarrow{a} \times \overrightarrow{b} \vert\]
\[\begin{align*} A_{BCHG} &= \vert \overrightarrow{CB} \times \overrightarrow{CH} \vert \\[0.8em] &= \vert (\overrightarrow{B} - \overrightarrow{C}) \times (\overrightarrow{H} - \overrightarrow{C}) \vert \\[0.8em] &= \left| \left[ \begin{pmatrix} 8 \\ 0 \\ 5 \end{pmatrix} - \begin{pmatrix} 8 \\ 10 \\ 5 \end{pmatrix} \right] \times \left[ \begin{pmatrix} 4 \\ 10 \\ 8 \end{pmatrix} - \begin{pmatrix} 8 \\ 10 \\ 5 \end{pmatrix} \right] \right| \\[0.8em] &= \left| \begin{pmatrix} 0 \\ -10 \\ 0 \end{pmatrix} \times \begin{pmatrix} -4 \\ 0 \\ 3 \end{pmatrix} \right| \\[0.8em] &= \left| \begin{pmatrix} (-10) & \cdot & 3 & - & 0 & \cdot & 0 \\ 0 & \cdot & (-4) & - & 0 & \cdot & 3 \\ 0 & \cdot & 0 & - & (-10) & \cdot & (-4) \end{pmatrix} \right| \\[0.8em] &= \left| \begin{pmatrix} -30 \\ 0 \\ -40 \end{pmatrix} \right| \\[0.8em] &= \sqrt{(-30)^2 + 0^2 + (-40)^2} \\[0.8em] &= \sqrt{2500} \\[0.8em] &= 50 \end{align*}\]
Der Flächeninhalt der Dachfläche, die im Modell durch das Rechteck \(BCHG\) dargestellt wird, beträgt 50 m2.


