Ein Glücksrad besteht aus zwei unterschiedlich großen Sektoren. Der größere Sektor ist mit der Zahl 1 und der kleinere mit der Zahl 3 beschriftet. Die Wahrscheinlichkeit dafür, beim einmaligen Drehen des Glücksrads die Zahl 1 zu erzielen, wird mit \(p\) bezeichnet. Das Glücksrad wird zweimal gedreht.
Begründen Sie, dass die Wahrscheinlichkeit dafür, dass die Summe der beiden erzielten Zahlen 4 ist, durch den Term \(2p \cdot (1- p)\) angegeben wird.
(1 BE)
Lösung zu Teilaufgabe a
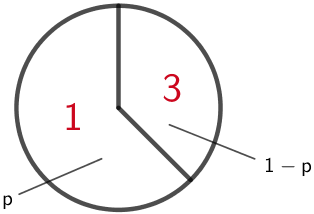
Das Glücksrad wird zweimal gedreht.
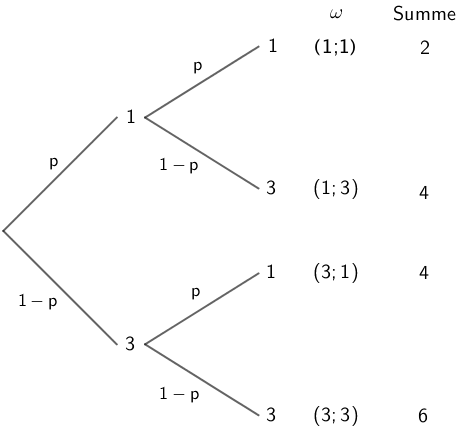
Veranschaulichung mithilfe eines Baumdiagramms
Unter Anwendung der ersten und der zweiten Pfadregel ergibt sich:
Pfadregeln
Verzweigungsregel (Knotenregel)
Die Summe der Wahrscheinlichkeiten an den Ästen, die von einem Knoten ausgehen, ist gleich eins.
1. Pfadregel (Produktregel)
Die Wahrscheinlichkeit eines Ergebnisses ist gleich dem Produkt der Wahrscheinlichkeiten entlang des Pfades, der zu dem Ergebnis führt.
2. Pfadregel (Summenregel)
Die Wahrscheinlichkeit eines Ereignisses ist gleich der Summe der Wahrscheinlichkeiten der Ergebnisse, die zu diesem Ereignis gehören.
\[\begin{align*} P(\text{„Summe ist 4"}) &= \underbrace{P(1;3) + P(3;1)}_{\large{\text{2. Pfadregel}}} \\[0.8em] &= \underbrace{p \cdot (1 - p)}_{\large{\text{1. Pfadregel}}} + \underbrace{(1 - p) \cdot p}_{\large{\text{1. Pfadregel}}} \\[0.8em] &= (p + p) \cdot (1 - p) \\[0.8em] &= 2p \cdot (1 - p) \end{align*}\]


