Eine Funktion der Form \(\displaystyle I_{a} \colon x \mapsto \int_{a}^{x} f(t)\, dt\) mit einer festen unteren Integrationsgrenze \(a \in D_{f}\) und einer variablen oberen Integrationsgrenze heißt Integralfunktion von \(f\) zur unteren Grenze \(a\).
Integralfreie Darstellung einer Integralfunktion
Es gilt:
\(\displaystyle I_{a}(x) = \int_{a}^{x} f(t)\, dt = F(x) - F(a)\), wobei \(F\) eine Stammfunktion von \(f\) ist.
Hauptsatz der Differential- und Integralrechnung (HDI)
Jede Integralfunktion \(\displaystyle I_{a} \colon x \mapsto \int_{a}^{x} f(t)\, dt\) einer stetigen Funktion \(f\) ist eine Stammfunktion von \(f\).
\[I_{a}(x) = \int_{a}^{x} f(t)\, dt \quad \Longrightarrow \quad I'_{a}(x) = f(x)\]
(vgl. Merkhilfe)
Beispiel:
Gegeben sei die in \(\mathbb R\) definierte Funktion \(f \colon x \mapsto x^{2}\).
Der Funktionsterm \(F(x)\) der Menge aller Stammfunktionen der Funktion \(f\) wird durch das unbestimmte Integral \(\displaystyle \int x^{2} \, dx\) beschrieben (vgl. Abiturskript - 1.6.2 Unbestimmtes Integral).
\[\int x^{2} \, dx = \frac{1}{2 + 1} \cdot x^{2 + 1} + C = \frac{1}{3}x^{3} + C\]
Vergleich mit der Integralfunktion \(\displaystyle I_{1}(x) = \int_{1}^{x} t^{2}\, dt\):
\[I_{1}(x) = \int_{1}^{x} t^{2}\, dt = \left[ \frac{1}{3}x^{3} \right]_{1}^{x} = \frac{1}{3}x^{3} - \frac{1}{3} \cdot 1^{3} = \frac{1}{3}x^{3} - \frac{1}{3}\]
Der Vergleich zeigt, dass die untere Integrationsgrenze der Integralfunktion \(\displaystyle I_{1}(x) = \int_{1}^{x} t^{2}\, dt\) die Integrationskonstante \(C\) der Menge aller Stammfunktionen \(\displaystyle \int x^{2} = \frac{1}{3}x^{3} + C\) mit dem Wert \(-\frac{1}{3}\) belegt.
Damit ist die Integralfunktion \(I_{1}(x)\) genau eine Stammfunktion der Funktion \(f\) und es gilt: \(I'_{1}(x) = f(x)\).
Nullstelle einer Integralfunktion
Jede Integralfunktion \(\displaystyle I_{a} \colon x \mapsto \int_{a}^{x} f(t)\, dt\) besitzt an der unteren Integrationsgrenze \(x = a\) eine Nullstelle.
\[I_{a}(a) = \int_{a}^{a} f(t) \, dt = F(a) - F(a) = 0\]
\(F\) ist eine Stammfunktion von \(f\).
Weitere wichtige Eigenschaften einer Integralfunktion
\(I'_{a}(x) = f(x) \quad \Longrightarrow \quad\)Nullstellen von \(f\) entsprechen Extrem- oder Terrassenstellen von \(I_{a}\).
\(I''_{a}(x) = f'(x) \quad \Longrightarrow \quad\)Extremstellen von \(f\) entsprechen Wendestellen von \(I_{a}\).
Zusammenhang Integralfunktion - Stammfunktion
Gemäß dem Hauptsatz der Differential- und Integralrechnung (HDI) ist jede Integralfunktion einer stetigen Funktion \(f\) eine Stammfunktion von \(f\). Umgekehrt gilt dies nicht, denn jede Integralfunktion von \(f\) hat mindestens eine Nullstelle, aber nicht jede Stammfunktion von \(f\) hat zwangsläufig eine Nullstelle.
Die Menge aller Stammfunktionen von \(f\) ist gegeben durch das unbestimmte Integral \(\displaystyle \int f(x) dx = F(x) + C\). Dabei bezeichnet \(F(x)\) den Funktionsterm einer Stammfunktion von \(f\) und \(C\) die sogenannte Integrationskonstante mit \(C \in \mathbb R\) (vgl. Abiturskript - 1.6.2 Unbestimmtes Integral).
Die Integrationskonstante \(C\) bewirkt eine Verschiebung des Graphen einer Stammfunktion von \(f\) in \(y\)-Richtung. Bewirkt die Verschiebung, dass der Graph einer Stammfunktion von \(f\) vollständig ober- oder unterhalb der \(x\)-Achse verläuft, besitzt die Stammfunktion keine Nullstelle und ist damit keine Integralfunktion von \(f\).
Beispiel:
Gegeben sei die in \(\mathbb R\) definierte und stetige Funktion \(f \colon x \mapsto x\).
Betrachtet wird beispielsweise die Integralfunktion \(\displaystyle I \colon x \mapsto \int_{0}^{x} f(t) dt\) der Funktion \(f\) sowie die Menge aller Stammfunktionen \(\displaystyle \int f(x) dx = F(x) + C\).
\[\int f(x) dx = \int x dx = \frac{1}{2}x^{2} + C\]
\[I(x) = \int_{0}^{x} f(t) dt = \left[ \frac{1}{2}x^{2} \right]_{0}^{x} = \frac{1}{2}x^{2} - \frac{1}{2} \cdot 0^{2} = \frac{1}{2}x^{2}\]
\(\displaystyle I(0) = \int_{0}^{0} = F(0) - F(0) = 0\) bzw. \(I(0) = \dfrac{1}{2} \cdot 0^{2} = 0\)
Die Integralfunktion \(I\) besitzt an der unteren Integrationsgrenze \(x = 0\) eine Nullstelle.
Dagegen besitzen alle Stammfunktionen \(x \mapsto \dfrac{1}{2}x^{2} + C\) von \(f\) für \(C \in \mathbb R^{+}\) keine Nullstelle, da der Graph einer Stammfunktion (nach oben geöffnete Parabel) für \(C \in \mathbb R^{+}\) die \(x\)-Achse nicht schneidet. Diese Stammfunktionen sind somit keine Integralfunktionen.
Alle Stammfunktionen \(x \mapsto \dfrac{1}{2}x^{2} + C\) von \(f\) mit \(C \in \mathbb R_{0}^{-}\) wiederum sind Integralfunktionen von \(f\), da sie mindestens eine Nullstelle besitzen.
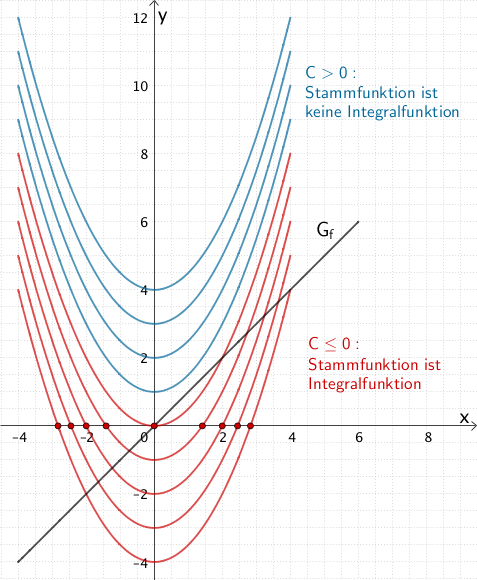
Graph \(G_{f}\) der Funktion \(f \colon x \mapsto x\) sowie Graphen der Stammfunktionen von \(f\) für \(C > 0\), die keine Integralfunktionen sind und Graphen der Stammfunktionen von \(f\) für \(C \leq 0\), die Nullstellen besitzen und deshalb Integralfunktionen sind.
Skizzieren des Graphen einer Integralfunktion
Im Gegensatz zum Skizzieren des Graphen einer Stammfunktion, genügt es beim Skizzieren des Graphen einer Integralfunktion nicht, nur den charakteristischen Verlauf des Graphen darzustellen (vgl. Abiturskript - 1.6.1 Stammfunktion, Skizzieren des Graphen einer Stammfunktion). Da eine Integralfunktion über einer Funktion \(f\) genau eine Stammfunktion der Menge aller möglicher Stammfunktionen einer Funktion \(f\) formuliert, ist der Graph einer Integralfunktion exakt festgelegt.
Beim Skizzieren einer Integralfunktion zum vorgegebenen Graphen einer Funktion \(f\) achtet man insbesondere auf die Nullstellen der Integralfunktion sowie auf die Null- und Extremstellen der Funktion \(f\).
Jeder Punkt des Graphen einer Integralfunktion kann mithilfe der Flächenbilanz der Fläche, welche \(G_{f}\) im entsprechenden Integrationsintervall mit der \(x\)-Achse einschließt, graphisch näherungsweise erarbeitet werden. So lässt sich beispielweise anhand einer Nullstelle von \(G_{f}\) auch näherungsweise die \(y\)-Koordinate eines Extrempunkts des Graphen einer Integralfunktion ermitteln.
Beispiel:
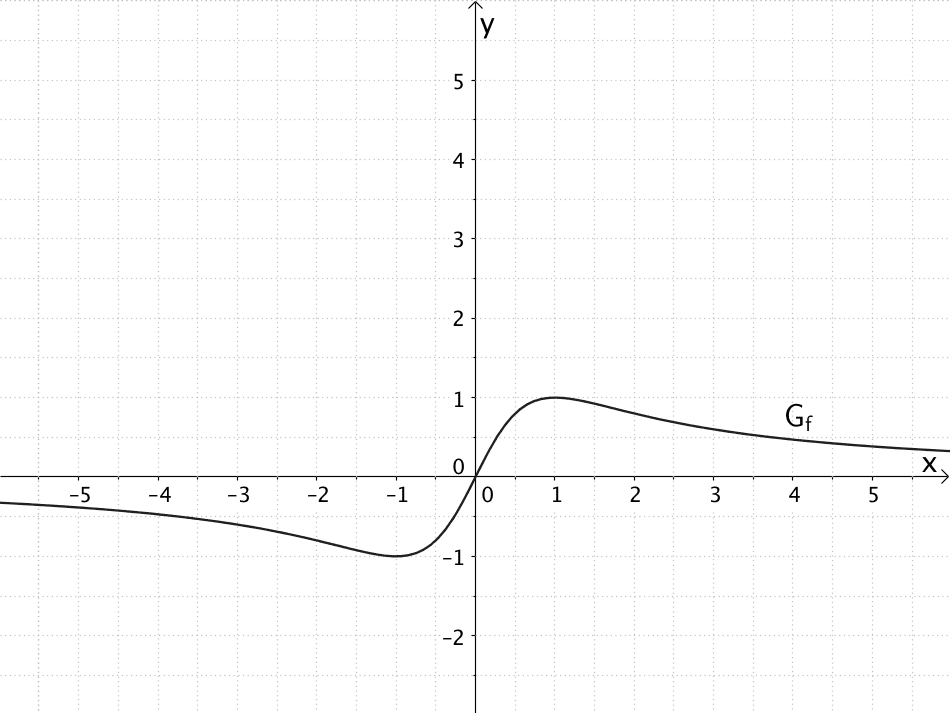
Die Abbildung zeigt den Graphen einer in \(\mathbb R\) definierten, zum Ursprung punktsymmetrischen, gebrochenrationalen Funktion \(f\).
Skizzieren Sie im gesamten dargestellten Bereich den Verlauf des Graphen der Integralfunktion \(\displaystyle I_{1} \colon x \mapsto \int_{1}^{x} f(t)\,dt\).
Nullstellen der Integralfunktion \(I_{1}(x)\)
Die Integralfunktion \(I_{1}(x)\) hat für \(x = 1\) eine Nullstelle.
\[I_{1}(1) = \int_{1}^{1} f(t)\, dt = F(1) - F(1) = 0\]
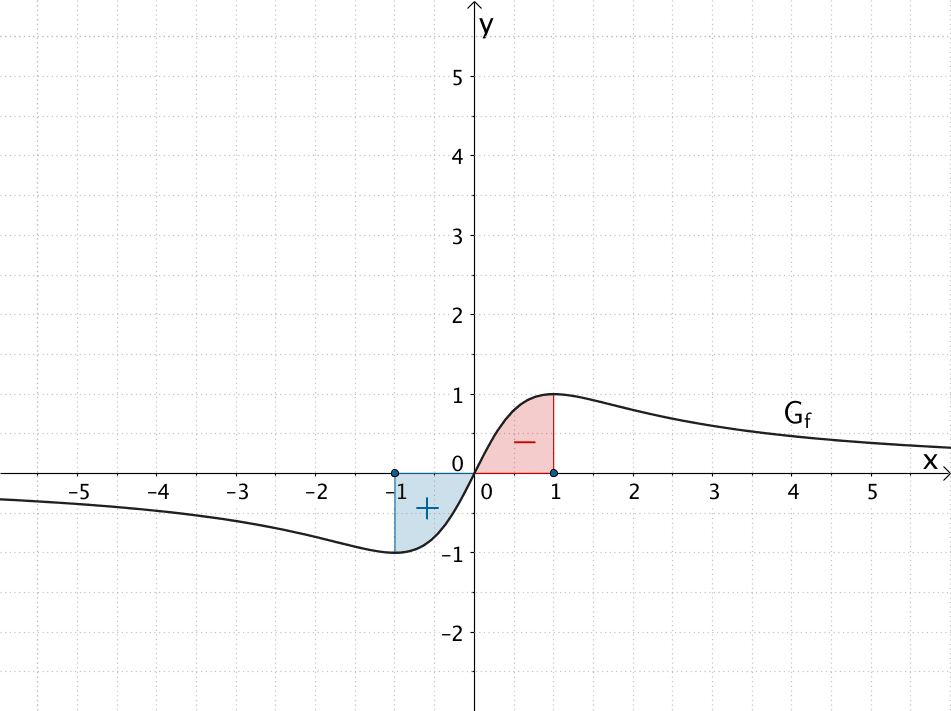
Eine weitere Nullstelle lässt sich mithilfe der Flächenbilanz der Fläche ausmachen, welche \(G_{f}\) mit der \(x\)-Achse einschließt.
Wegen der Punktsymmetrie von \(G_{f}\) hat das Flächenstück, welches \(G_{f}\) im Intervall \([0;1]\) mit der \(x\)-Achse einschließt, den gleichen Flächeninhalt wie das Flächenstück, welches \(G_{f}\) im Intervall \([-1;0]\) mit der \(x\)-Achse einschließt. Da die betrachteten Flächen einmal oberhalb und einmal unterhalb der \(x\)-Achse liegen, gehen sie in die Flächenbilanz mit unterschiedlichem Vorzeichen ein.
Somit ist die Flächenbilanz der Fläche, welche \(G_{f}\) im Intervall \([-1;1]\) mit der \(x\)-Achse einschließt gleich Null.
\[\Longrightarrow \quad I_{1}(-1) = \int_{1}^{-1}f(t)\,dt = 0\]
Da „nach links" integriert wird (obere Integrationsgrenze kleiner als untere Integrationsgrenze) zählt das oberhalb der \(x\)-Achse liegende Flächenstück im Intervall \([0;1]\) negativ und das unterhalb der \(x\)-Achse liegende Flächenstück im Intervall \([-1;0]\) positiv.
Extremstelle der Integralfunktion \(I_{1}(x)\)
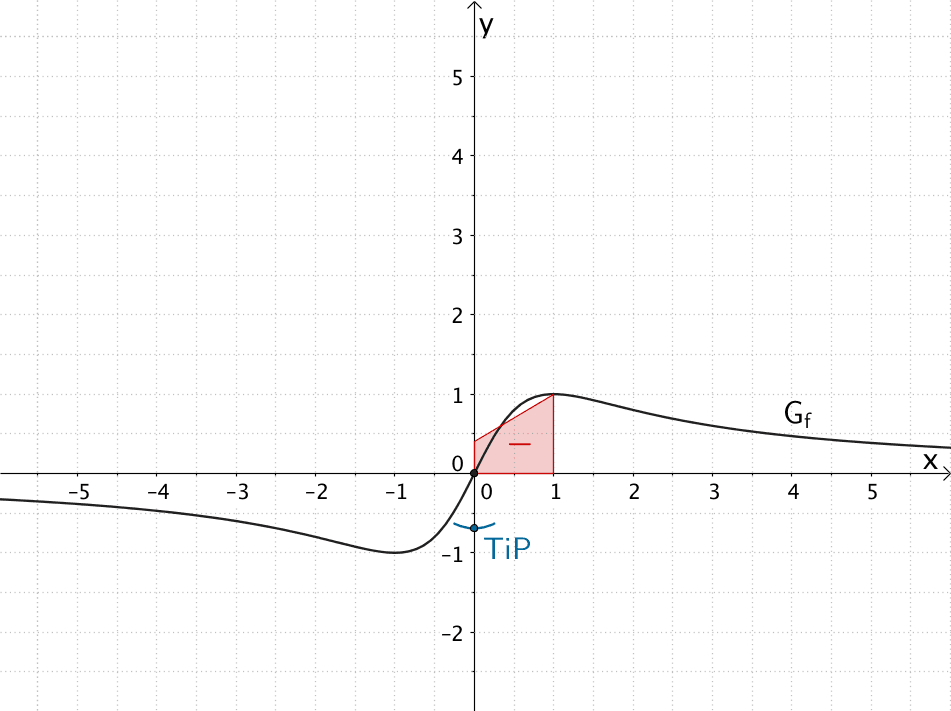
Der Graph der Funktion \(f\) hat an der Stelle \(x = 0\) eine einfache Nullstelle mit Vorzeichenwechsel von \(-\) nach \(+\).
Mit \(I'_{1}(0) = f(0) = 0\) folgt daraus, dass der Graph der Integralfunktion \(I_{1}\) an der Stelle \(x = 0\) einen Tiefpunkt \(TiP\) besitzt (vgl. Abiturskript - 1.5.3 Monotonieverhalten, Extrem- und Terrassenpunkte).
\[\left. \begin{align*} &I_{1}'(x) < 0 \; \text{für}\; x < 0 \\[0.8em] &I'_{1}(0) = 0 \\[0.8em] &I'_{1}(x) > 0 \; \text{für}\; x > 0 \end{align*} \right\} \enspace \Rightarrow \enspace \text{Tiefpunkt}\; TiP\]
Die \(y\)-Koordinate des Tiefpunkts kann auf geometrischem Wege näherungsweise abgeschätzt werden, indem man den Flächeninhalt betrachtet, welcher dem Wert des Integrals \(\displaystyle \int_{1}^{0}f(t)\,dt\) entspricht. Beispielsweise lässt sich die Fläche, welche \(G_{f}\) im Intervall \([0;1]\) mit der \(x\)-Achse einschließt, durch ein Trapez mit den Längen der Grundlinien 0,4 LE (Längeneinheiten) bzw. 1 LE sowie einer Höhe von 1 LE annähern. Da mit \(\displaystyle \int_{1}^{0}f(t)\,dt\) „nach links" integriert wird (obere Integrationsgrenze kleiner als untere Integrationsgrenze), zählt der Flächeninhalt der oberhalb der \(x\)-Achse liegenden Fläche negativ.
\[\Longrightarrow \quad \int_{1}^{0} f(t)\,dt \approx -\frac{0{,}4 + 1}{2} \cdot 1 = -0{,}7 \quad \Longrightarrow \quad TiP(0|-0{,}7)\]
Wendestellen der Integralfunktion \(I_{1}(x)\)
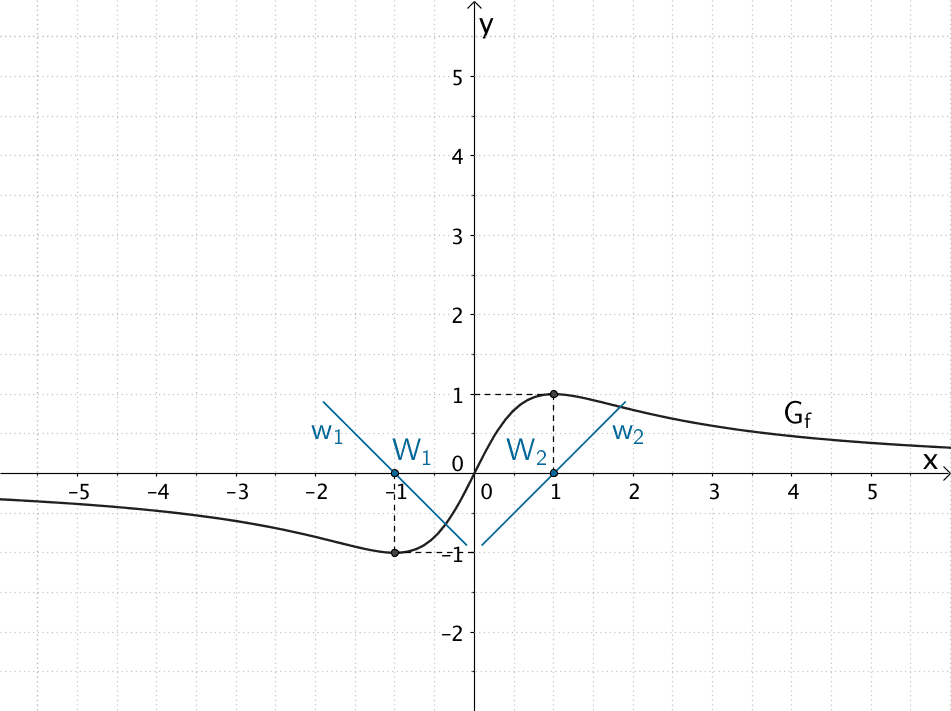
An der Stelle \(x = -1\) und \(x = 1\) hat der Graph der Funktion \(f\) jeweils einen Extrempunkt.
Mit \(I''_{1}(-1) = f'(-1) = 0\) und \(I''_{1}(1) = f'(1) = 0\) folgt daraus, dass der Graph der Integralfunktion \(I_{1}\) an der Stelle \(x = -1\) und \(x = 1\) jeweils eine Wendestelle besitzt. Die Wendestellen sind zugleich Nullstellen (vgl. Nullstellen der Integralfunktion \(I_{1}\)), d.h. es ergeben sich die Wendepunkte \(W_{1}(-1|0)\) und \(W_{2}(1|0)\).
MIt \(I'_{1}(-1) = f(-1) = -1\) und \(I'_{1}(1) = f(1) = 1\) kann die Steigung der Wendetangenten \(w_{1}\) und \(w_{2}\) jeweils angegeben werden.
\[m_{w_{1}} = I'_{1}(-1) = -1\]
\[m_{w_{2}} = I'_{1}(1) = 1\]
Krümmungsverhalten des Graphen der Integralfunktion \(I_{1}\) (vgl. Abiturskript - 1.5.4 Krümmungsverhalten und Wendepunkte):
Im Intervall \(]-\infty;-1[\) fällt \(G_{f}\), also gilt \(f'(x) < 0\).
\(\Longrightarrow \quad I''_{1}(x) = f'(x) < 0\) für \(x \in \;]-\infty;-1[\)
\(\Longrightarrow \quad\) Der Graph der Integralfunktion \(I_{1}\) ist im Intervall \(]-\infty;-1[\) rechtsgekrümmt.
Im Intervall \(]-1;1[\) steigt \(G_{f}\), also gilt \(f'(x) > 0\).
\(\Longrightarrow \quad I''_{1}(x) = f'(x) > 0\) für \(x \in \;]-1;1[\)
\(\Longrightarrow \quad\) Der Graph der Integralfunktion \(I_{1}\) ist im Intervall \(]-1;1[\) linksgekrümmt.
Im Intervall \(]1;+\infty[\) fällt \(G_{f}\), also gilt \(f'(x) < 0\).
\(\Longrightarrow \quad I''_{1}(x) = f'(x) < 0\) für \(x \in \;]1;+\infty[\)
\(\Longrightarrow \quad\) Der Graph der Integralfunktion \(I_{1}\) ist im Intervall \(]1;+\infty[\) rechtsgekrümmt.
Weitere Punkte des Graphen der Integralfunktion \(I_{1}\)
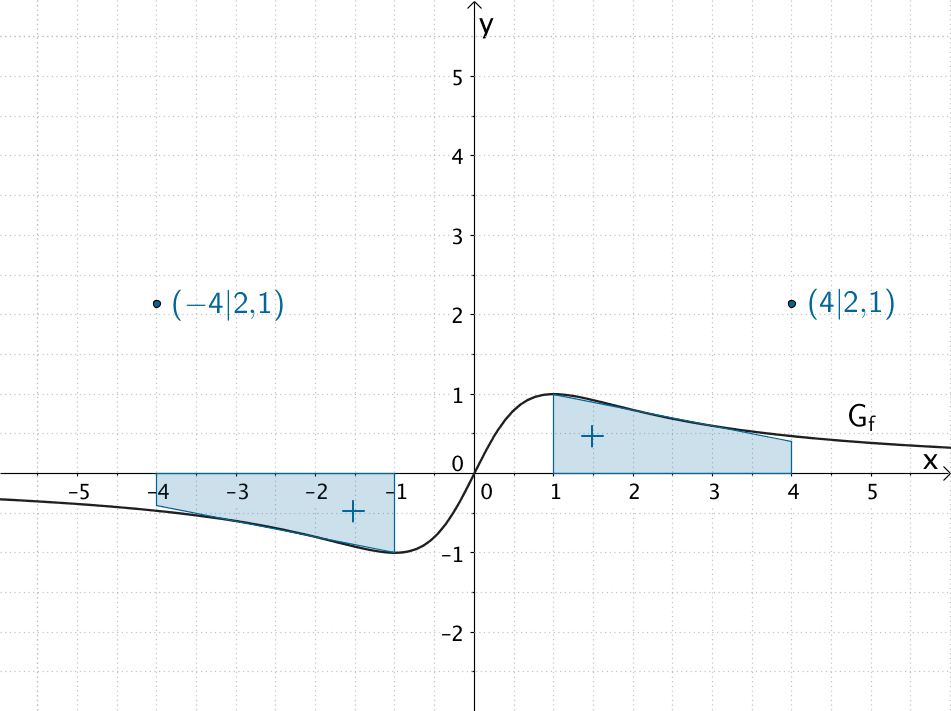
Mithilfe der Flächenbilanz der Fläche, welche \(G_{f}\) mit der \(x\)-Achse einschließt, lassen sich für \(x < -1\) bzw. \(x > 1\) weitere Punkte des Graphen der Integralfunktion graphisch näherungsweise ermitteln.
Beispielsweise lässt sich die Fläche, welche \(G_{f}\) im Intervall \([-4;-1]\) und im Intervall \([1;4]\) mit der \(x\)-Achse einschließt, durch Trapeze mit den Längen der Grundlinien 0,4 LE (Längeneinheiten) bzw. 1 LE sowie jeweils einer Höhe von 3 LE annähern.
Damit ergibt sich näherungsweise:
\[I_{1}(4) = \int_{1}^{4}f(t)\,dt \approx \frac{1 + 0{,}4}{2} \cdot 3 = 2{,}1\]
\[\begin{align*}I_{1}(-4) &= \int_{1}^{-4} f(t)\,dt = \int_{1}^{-1} f(t) + \int_{-1}^{-4} f(t)\,dt \\[0.8em] &= 0 + \int_{-1}^{-4} f(t)\,dt \\[0.8em] &\approx \frac{1 + 0{,}4}{2} \cdot 3 = 2{,}1 \end{align*}\]
Der Funktionswert \(I_{1}(-4)\) ist positiv, da „nach links" integriert wird (obere Inetrgationsgyrenze kleiner als untere Integrationsgrenze) und die Fläche, welche \(G_{f}\) im Intervall{[-4;-1]} mit der \(x\)-Achse einschließt, unterhalb der \(x\)-Achse liegt.
Zusammenfassung der Ergebnisse
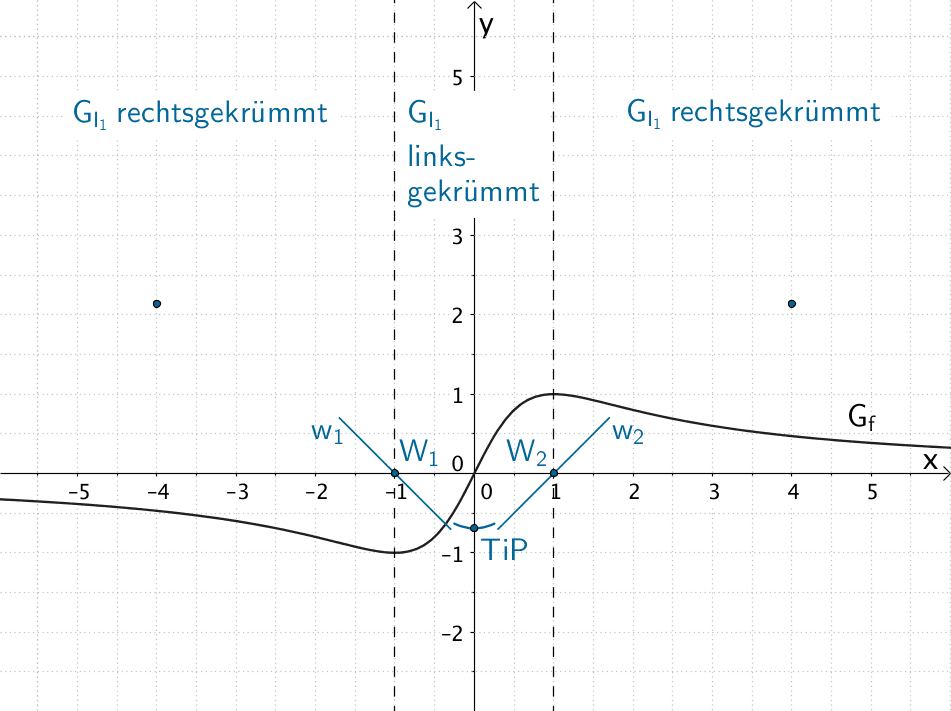
Tiefpunkt \(TiP(0|-0{,}7)\), Wendepunkte \(W_{1}(-1|0)\) und \(W_{2}(1|0)\) (Wendepunkte zugleich Nullstellen), Krümmungsverhalten sowie weitere Punkte \((-4|2{,}1)\) und \((4|2{,}1)\) des Graphen \(G_{I_{1}}\) der Integralfunktion \(I_{1}\)
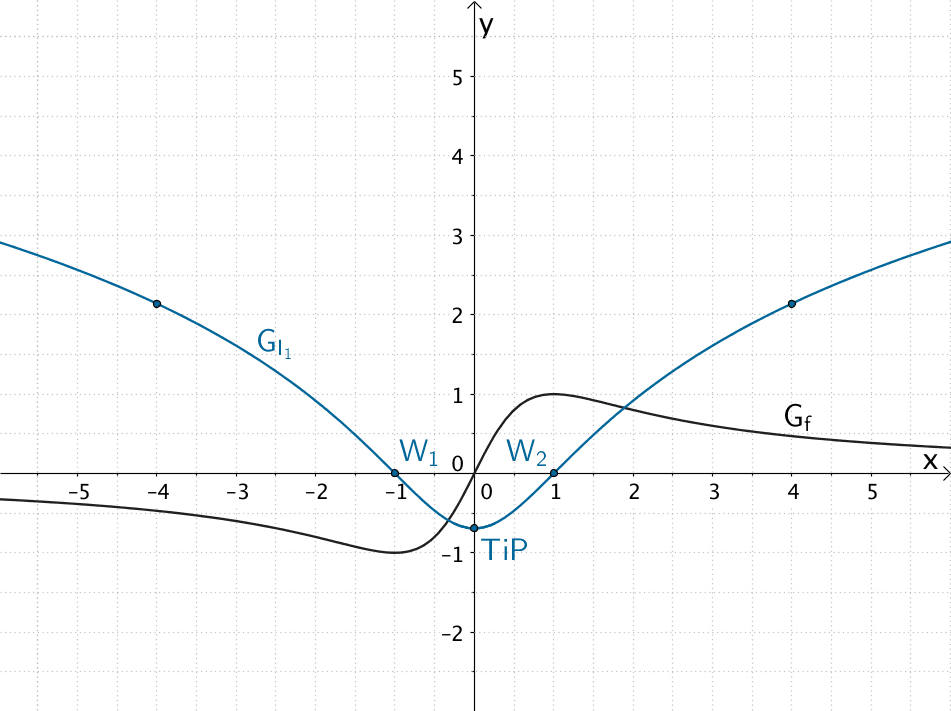
Verlauf des Graphen \(G_{I_{1}}\) der Integralfunktion \(\displaystyle I_{1} \colon x \mapsto \int_{1}^{x} f(t)\, dt\)
Beispielaufgabe
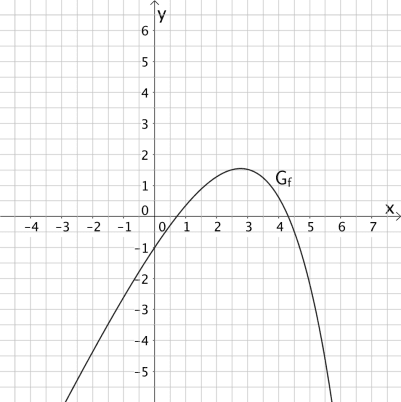
Die Abbildung zeigt den Graph der Funktion \(f\).
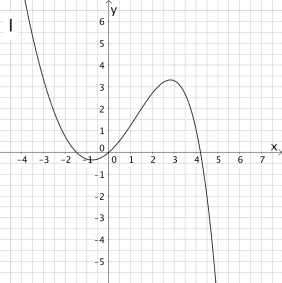
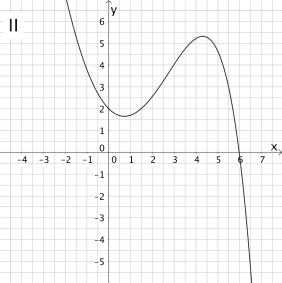
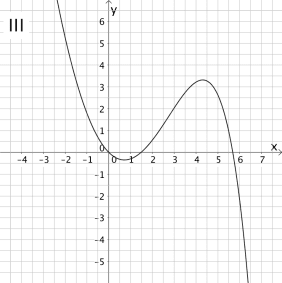
Entscheiden Sie, welcher der nachfolgenden Graphen I - IV den Verlauf des Graph der Integralfunktion \(\displaystyle I_{0} \colon x \mapsto \int_{0}^{x} f(t)\, dt\) abbildet und begründen Sie Ihre Wahl.
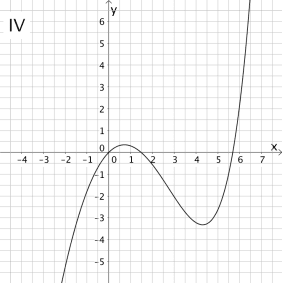
Mögliche Vorgehensweise
Nullstellen der Integralfunktion \(I_{0}\)
Die Integralfunktion \(I_{0}\) hat an der unteren Integrationsgrenze \(x = 0\) eine Nullstelle (vgl. Nullstelle einer Integralfunktion).
\[I_{0}(0) = \int_{0}^{0} f(t)\,dt = F(0) - F(0) = 0\]
\(\Longrightarrow \quad\)Graph II kommt nicht in Frage.
![Flächenbilanz der Flächen, welche der Graph der Funktion f im Intervall [0;1,5] mit der x-Achse einschließt. Flächenbilanz der Flächen, welche der Graph der Funktion f im Intervall [0;1,5] mit der x-Achse einschließt.](/images/stories/abi_check/analysis/Int_IntFunk_Bsp6.png)
Der Graph der Funktion \(f\) schließt im Intervall \([0;1{,}5]\) zwei Flächenstücke mit annähernd gleichem Flächeninhalt ein. Da die Flächenstücke einmal unterhalb und einmal oberhalb der \(x\)-Achse liegen, gehen sie in die Flächenbilanz mit unterschiedlichem Vorzeichen ein. Folglich ist die Flächenbilanz gleich Null.
\[\Longrightarrow \quad I_{0}(1{,}5) = \int_{0}^{1{,}5} f(t)\,dt \approx 0 \]
Die Integralfunktion \(I_{0}\) hat mit \(x \approx 1{,}5\) eine weitere Nullstelle.
\(\Longrightarrow \quad \)Graph I kommt nicht in Frage.
Extremstellen der Integralfunktion \(I_{0}\)
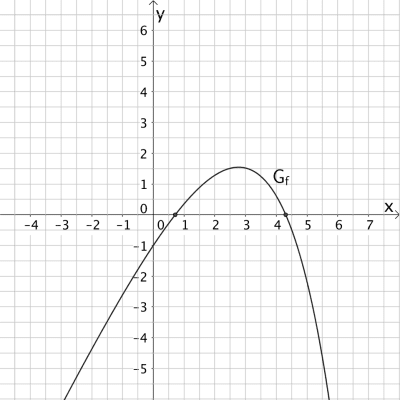
Der Graph der Funktion \(f\) hat für \(x \approx 0{,}7\) eine einfache Nullstelle mit Vorzeichenwechsel von \(-\) nach \(+\) und für \(x \approx 4{,}3\) eine einfache Nullstelle mit Vorzeichenwechsel von \(+\) nach \(-\).
Mit \(I'_{0}(0{,}7) = f(0{,}7) \approx 0\) und \(I'_{0}(4{,}3) = f(4{,}3) \approx 0\) folgt daraus, dass der Graph der Integralfunktion \(I_{0}\) an der Stelle \(x \approx 0{,}7\) einen Tiefpunkt und an der Stelle \(x \approx 4{,}3\) einen Hochpunkt besitzt.
\(\Longrightarrow \quad\)Graph III bildet den Graph der Integralfunktion \(I_{0}\) ab.
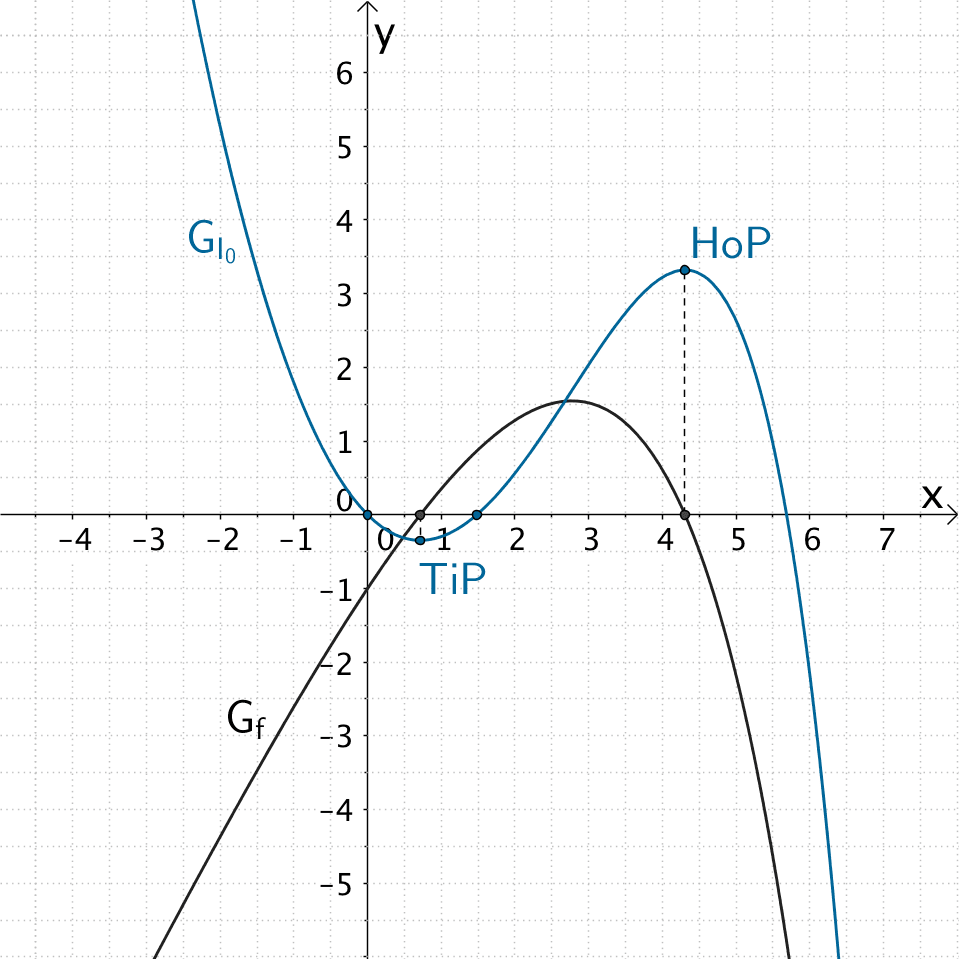
Graph der Funktion \(f\) und Graph der Integralfunktion \(\displaystyle I_{0} \colon x \mapsto \int_{0}^{x} f(t)\, dt\)

