Ordnen Sie die Graphen I bis VI den freien Feldern der Tabelle so zu, dass unter einem Funktionsgraphen jeweils der Graph seiner Ableitung zu sehen ist und beschriften Sie die Felder entsprechend. Begründen Sie Ihre Wahl für die erste Spalte.
Hinweis: Die Skalierung der Koordinatenachsen ist für alle abgebildeten Graphen dieselbe.
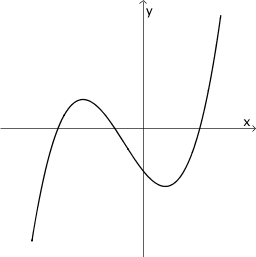 |
||
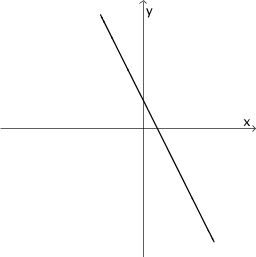 |
||
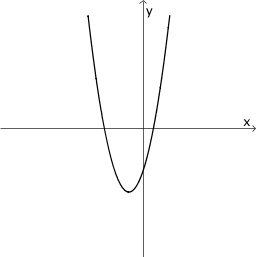 |
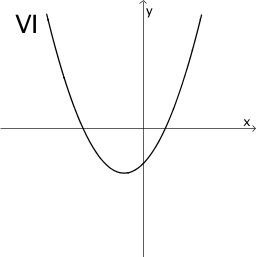
Graphen I bis VI:
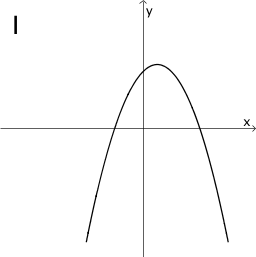 |
 |
 |
 |
 |
 |
Zuordnung der Graphen I bis VI
 |
 |
 |
 |
 |
 |
 |
 |
 |
Begründung der Zuordnung für die erste Spalte
Um von dem Graphen einer Funktion auf den Graphen der zugehörigen Ableitungsfunktion zu schließen, betrachtet man die Lage der Extrempunkte des Graphen der Funktion und das Monotonieverhalten in der Umgebung der Extrempunkte.
Anwendung der Differentialrechnung:
Extrempunkte
Ist \(f'(x_{0}) = 0\) und wechselt \(f'\) an der Stelle \(x_{0}\) das Vorzeichen, so hat \(G_{f}\) an der Stelle \(x_{0}\) einen Extrempunkt.
(vgl. Merkhilfe)
Anwendung der Differetialrechnung:
Monotoniekriterium
\(\textcolor{#cc071e}{f'(x) < 0}\) im Intervall \( I \; \Rightarrow \; G_{f}\) fällt streng monoton in \(I\)
\(\textcolor{#0087c1}{f'(x) > 0}\) im Intervall \( I \; \Rightarrow \; G_{f}\) steigt streng monoton in \(I\)
(vgl. Merkhilfe)
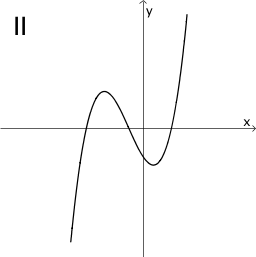
Der Funktionsgraph in der ersten Spalte oben zeigt für einen negativen \(x\)-Wert einen Hochpunkt und für einen positiven \(x\)-Wert einen Tiefpunkt. An diesen Extremstellen besitzt der Graph eine waagrechte Tangente. In der Umgebung des Hochpunkts zeigt der Graph einen Wechsel des Monotonieverhaltens von streng monoton steigend nach streng monoton fallend und in der Umgebung des Tiefpunkts von streng monoton fallend nach streng monoton steigend Folglich hat der Graph der zugehörigen Ableitungsfunktion an der Stelle des Hochpunkts eine Nullstelle mit Vorzeichenwechsel von \(+\) nach \(-\) und an der Stelle des Tiefpunkts eine Nullstelle mit Vorzeichenwechsel von \(-\) nach \(+\).
Von den Graphen I bis VI bestätigt ausschließlich Graph IV das beschriebene Verhalten.
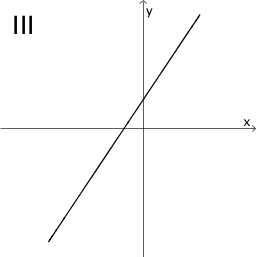
Graph IV zeigt für einen negativen \(x\)-Wert als einzigen Extrempunkt einen Tiefpunkt. An der Stelle des Tiefpunkts besitzt Graph IV eine waagrechte Tangente. In der Umgebung des Tiefpunkts zeigt Graph IV einen Wechsel des Monotonieverhaltens von streng monoton fallend nach streng monoton steigend. Folglich hat der Graph der zugehörigen Ableitungsfunktion an der Stelle des Tiefpunkts von Graph IV eine einzige Nullstelle mit Vorzeichenwechsel von \(-\) nach \(+\).
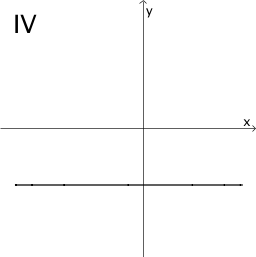
Von den verbleibenden Graphen I bis III sowie V und VI bestätigt ausschließlich Graph III das beschriebene Verhalten.

