Zeichnen Sie den Graphen der Umkehrfunktion von \(h^{*}\) unter Verwendung der bisherigen Ergebnisse, insbesondere der Lage von Punkt \(S\), in Abbildung 1 ein.
(3 BE)
Lösung zu Teilaufgabe 1e
Graph einer Umkehrfunktion
Umkehrfunktion \(\boldsymbol{f^{-1}}\) einer Funktion \(\boldsymbol{f}\)
Bestimmung des Funktionsterms \(\boldsymbol{f^{-1}(x)}\)
1. Funktionsgleichung \(\,y = f(x)\,\) nach \(\,x\,\) auflösen
2. Variablen tauschen: \(\;x \longleftrightarrow y \quad \Longrightarrow \quad y = f^{-1}(x)\)
Es gilt: \(\;D_{f^{-1}} = W_f\;\) und \(\; W_{f^{-1}} = D_f\)
Graph der Umkehrfunktion
Die Graphen einer Funktion und ihrer Umkehrfunktion sind zueinander symmetrisch bzgl. der Winkelhalbierenden des I. und III. Quadranten mit der Gleichung \(y = x\).
Der Graph der Umkehrfunktion \(h^{*^{-1}}\) geht durch Spiegelung des Graphen der Funktion \(h^{*}\) an der Winkelhalbierenden \(w\) des ersten und dritten Quadranten mit der Gleichung \(y = x\) hervor.
In Teilaufgabe 1d wurde der Schnittpunkt \(S\) des Graphen der Funktion \(h^{*}\) und der Winkelhalbierenden \(w\) berechnet. Der Graph der Umkehrfunktion \(h^{*^{-1}}\) und der Graph der Funktion \(h^{*}\) schneiden sich im Punkt \(S\). Der Punkt \(S\) ist Fixpunkt der Spiegelung des Graphen der Funktion \(h^{*}\) an der Winkelhalbierenden \(w\).
Bisherige Ergebnisse:
- \[D_{h^{*^{-1}}} = [-3;+\infty[; \; W_{h^{*^{-1}}} = [1;+\infty[\]
- Schnittpunkt \(S\left( e^{\frac{4}{3}} \Big| e^{\frac{4}{3}} \right)\) des Graphen der Funktion \(h^{*}\) und der Winkelhalbierenden \(w \colon y = x\)
Graph der Funktion \(h^{*}\) an der Winkelhalbierenden \(w\) spiegeln:
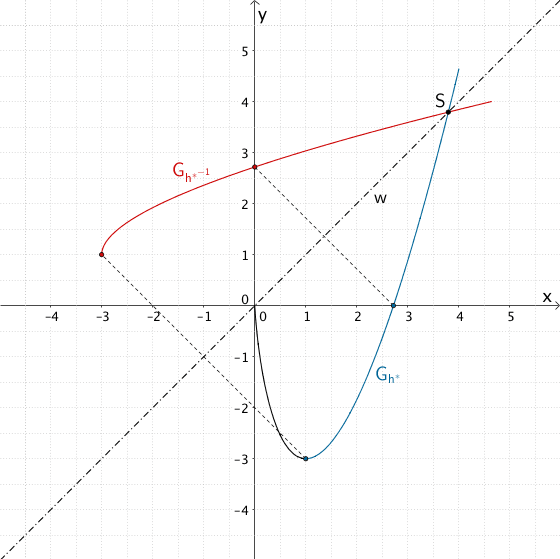
Zum Zeichnen der Spiegelung des Graphen der Funktion \(h^{*}\) an der der Winkelhalbierenden \(w \colon y = x\) des ersten und dritten Quadranten eigenen sich die Punkte \((1|-3)\) (vgl. Teilaufgabe 1b) und \((e|0)\) (vgl. Teilaufgabe 1a), sowie der Fixpunkt \(S\) (vgl. Teilaufgabe 1d)
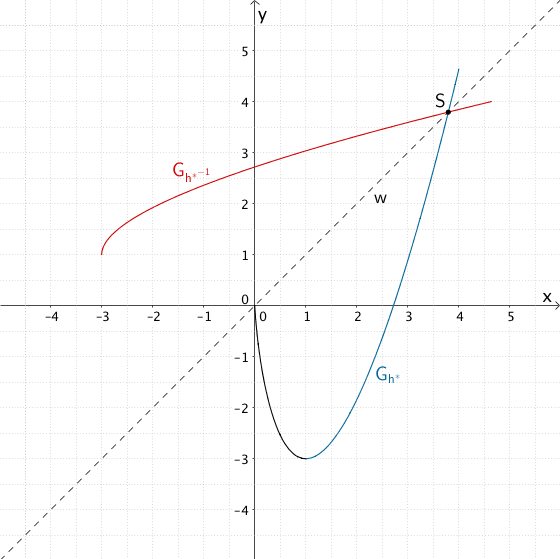
Graph der Funktion \(h^{*}\) und Graph der Umkehrfunktion \(h^{*^{-1}}\), Schnittpunkt \(S\) der Graphen \(G_{h^{*}}\) und \(G_{h^{}*^{-1}}\) bzw. der Winkelhalbierenden \(w\)


