Abbildung 2 zeigt den Graphen der in \(\mathbb R\) definierten Funktion \(g\), dessen einzige Extrempunkte \((-1|1)\) und \((0|0)\) sind, sowie den Punkt \(P\).
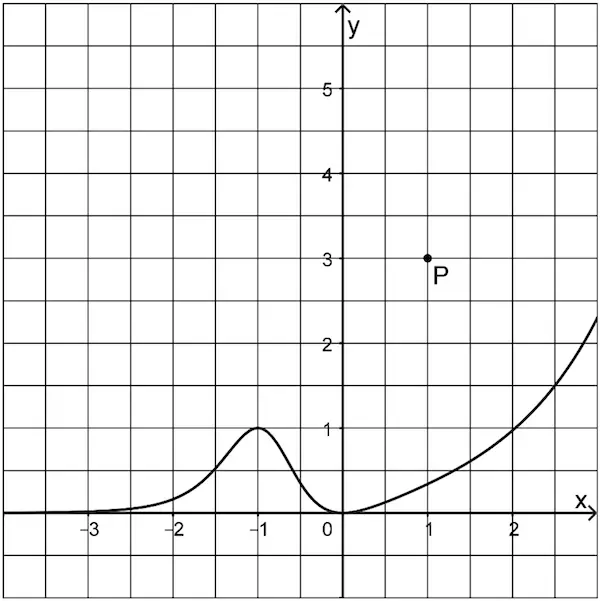Abb. 2
Geben Sie die Koordinaten des Tiefpunkts des Graphen der in \(\mathbb R\) definierten Funktion \(h(x) = -g(x - 3)\) an.
(2 BE)
Lösung zu Teilaufgabe 4a
\[h(x) =-g(x-3)\]
Koordinaten des Tiefpunkts des Graphen von \(h\): \((2|-1)\)
Ausführliche Erklärung (nicht verlangt)
Spiegeln von Funktionsgraphen
Spiegelung an der \(x\)-Achse: \(g(x) = -f(x)\)
Spiegelung an der \(y\)-Achse: \(h(x) = f(-x)\)
\[h(x) =\textcolor{#cc071e}{\boldsymbol{-}}g(\textcolor{#0087c1}{x-3})\]
Verschieben von Funktionsgraphen
\[g(x) = f(x +a) + b\]
Verschiebung in \(x\)-Richtung um \(-a\), Verschiebung in \(y\)-Richtung um \(b\)
Der Graph der Funktion \(h\) geht aus dem Graphen der Funktion \(g\) durch
- Spiegelung an der \(\textcolor{#cc071e}{x}\)-Achse und
- Verschiebung um 3 LE in positive \(\textcolor{#0087c1}{x}\)-Richtung
hervor.
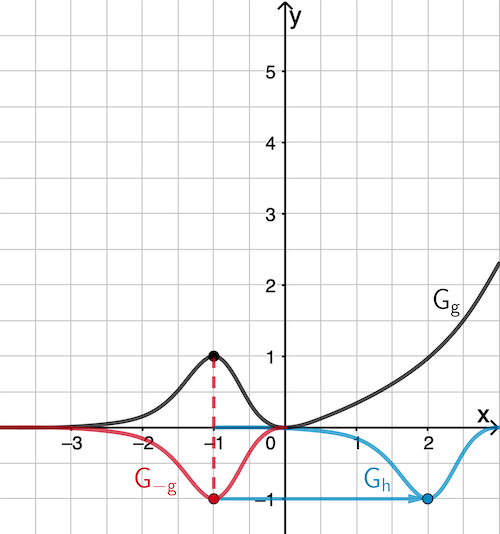
Durch die Spiegelung an der \(\textcolor{#cc071e}{x}\)-Achse wird der Hochpunkt \((-1|1)\) von \(G_g\) zum Tiefpunkt \(\textcolor{#cc071e}{(-1|-1)}\) von \(\textcolor{#cc071e}{G_{-g}}\).
Durch die Verschiebung um 3 LE in positive \(\textcolor{#0087c1}{x}\)-Richtung ergibt sich der Tiefpunkt \(\textcolor{#0087c1}{(2|-1)}\) von \(\textcolor{#0087c1}{G_h}\).
