Von den im einleitenden Text angegebenen Zahlenwerten soll nur der Prozentsatz 40 % so geändert werden, dass die Ereignisse \(A\) und \(R\) unabhängig sind. Geben Sie den geänderten Wert an.
(2 BE)
Lösung zu Teilaufgabe d
Der im einleitenden Text angegebene Prozentsatz 40 % (siehe Teilaufgabe a) gibt den Wert der bedingten Wahrscheinlichkeit \(P_A(\overline{R})\) an.
Begründung mit Baumdiagramm:
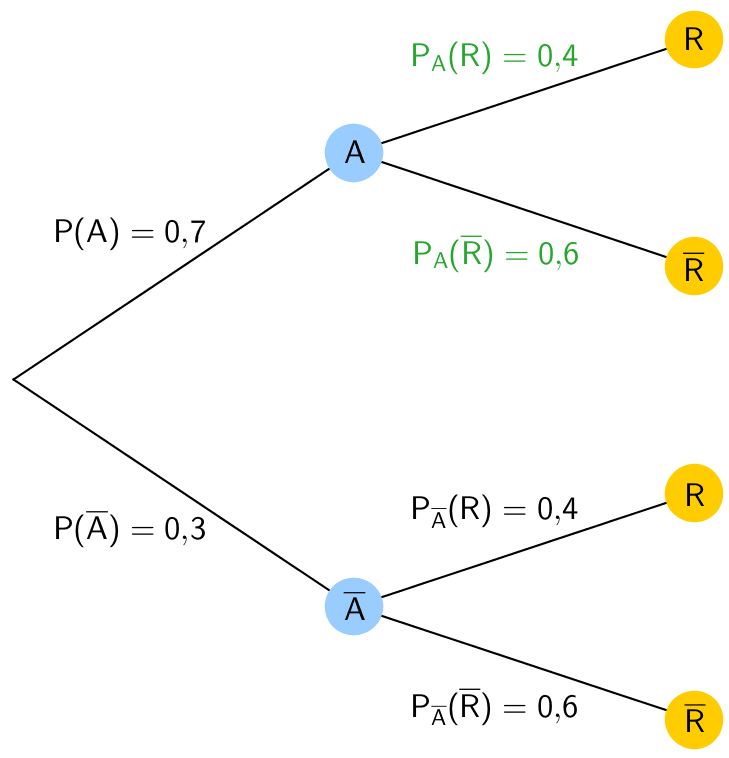
Die Ereignisse \(A\) und \(R\) sind stochastisch unabhängig, wenn die Wahrscheinlichkeiten an den Ästen der zweiten Stufe des Baumdiagramms gleich sind.
\[\Longrightarrow \quad P_A(\overline{R}) = P_{\overline{A}}(\overline{R}) = 0{,}6 = 60\,\%\]
Der im einleitenden Text angegebene Prozentsatz 40 % für die bedingte Wahrscheinlichkeit \(P_A(\overline{R})\) muss auf 60 % geändert werden, damit die Ereignisse \(A\) und \(R\) stochastisch unabhängig sind.


