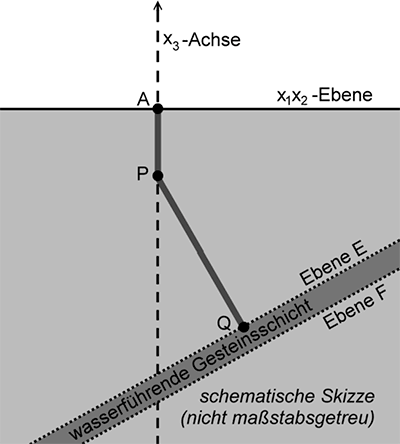
Eine Geothermieanlage fördert durch einen Bohrkanal heißes Wasser aus einer wasserführenden Gesteinsschicht an die Erdoberfläche. In einem Modell entspricht die \(x_{1}x_{2}\)-Ebene eines kartesischen Koordinatensystems der horizontal verlaufenden Erdoberfläche. Eine Längeneinheit im Koordinatensystem entspricht einem Kilometer in der Realität. Der Bohrkanal besteht aus zwei Abschnitten, die im Modell vereinfacht durch die Strecken \([AP]\) und \([PQ]\) mit den Punkten \(A(0|0|0)\), \(P(0|0|-1)\) und \(Q(1|1|-3{,}5)\) beschrieben werden (vgl. Abbildung).
Berechnen Sie auf der Grundlage des Modells die Gesamtlänge des Bohrkanals auf Meter gerundet.
(2 BE)
Lösung zu Teilaufgabe a
Auf der Grundlage des Modells ist die Gesamtlänge des Bohrkanals gleich der Summe der Längen der Strecken \([AP]\) und \([PQ]\) in Kilometer (vgl. Abbildung).
\(A(0|0|0)\), \(P(0|0|-1)\), \(Q(1|1|-3{,}5)\)
Betrag eines Vektors
\[ \vert \overrightarrow{a} \vert = \sqrt{\overrightarrow{a} \circ \overrightarrow{a}} = \sqrt{{a_1}^2 + {a_2}^2 + {a_3}^2}\]
(vgl. Merkhilfe)
\[\begin{align*} \overline{AP} + \overline{PQ} &= \vert \overrightarrow{AP} \vert + \vert \overrightarrow{PQ} \vert \\[0.8em] &= \vert \overrightarrow{P} - \overrightarrow{A} \vert + \vert \overrightarrow{Q} - \overrightarrow{P} \vert \\[0.8em] &= \left| \begin{pmatrix} 0 \\ 0 \\ -1 \end{pmatrix} - \begin{pmatrix} 0 \\ 0 \\ 0 \end{pmatrix} \right| + \left| \begin{pmatrix} 1 \\ 1 \\ -3{,}5 \end{pmatrix} - \begin{pmatrix} 0 \\ 0 \\ -1 \end{pmatrix} \right| \\[0.8em] &= \left| \begin{pmatrix} 0 \\ 0 \\ -1 \end{pmatrix} + \begin{pmatrix} 1 \\ 1 \\ -2{,}5 \end{pmatrix} \right| \\[0.8em] &= \sqrt{0^{2} + 0^{2} + (-1)^{2}} + \sqrt{1^{2} + 1^{2} + (-2{,}5)^{2}} \\[0.8em] &= 1 + \sqrt{8{,}25} \\[0.8em] &\approx 3{,}872 \end{align*}\]
Eine Längeneinheit entspricht einem Kilometer (vgl. Angabe).
\[3{,}872 \cdot 1000\,\text{m} = 3872\,\text{m}\]
Die Gesamtlänge des Bohrkanals beträgt etwa 3872 m.


