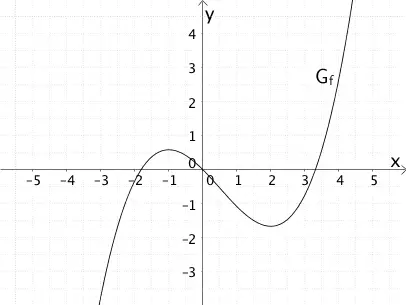
Die Abbildung zeigt den Graphen \(G_{f}\) einer Funktion \(f\).

Ordnen Sie dem Graphen der Funktion \(f\) aus den Graphen I bis VI den Graphen der zugehörigen Ableitungsfunktion \(f'\) und einer zugehörigen Stammfunktion \(F\) zu. Begründen Sie Ihre Wahl.

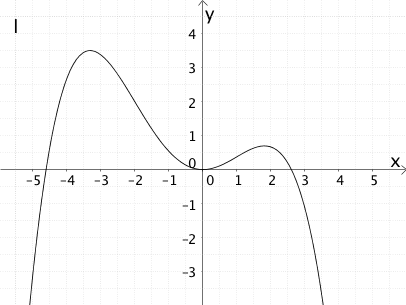
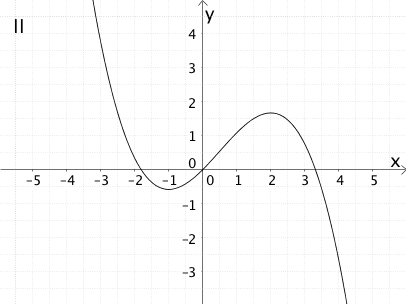
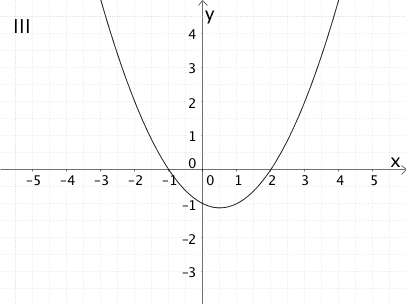
Graph der zugehörigen Ableitungsfunktion \(f'\)

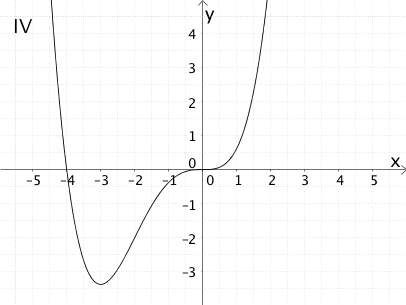
Graph III zeigt den Graphen der zugehörigen Ableitungsfunktion \(f'\) von \(f\).

Begründung:

Um von einem Graphen \(G_{f}\) einer Funktion \(f\) auf den Graphen \(G_{f'}\) der zugehörigen Ableitungsfunktion \(f'\) zu schließen, werden insbesondere die Extrempunkte von \(G_{f}\) und der Verlauf von \(G_{f}\) (Steigung, Monotonieverhalten) in der Umgebung der Extrempunkte betrachtet.

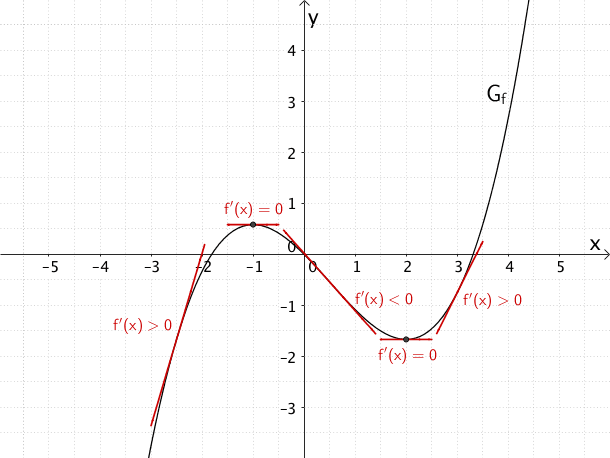
Der Graph \(G_{f}\) der Funktion \(f\) besitzt an der Stelle \(x = -1\) einen Hochpunkt und an der Stelle \(x = 2\) einen Tiefpunkt.

Die erste Ableitung \(f'\) der Funktion \(f\) beschreibt die Steigung einer Tangente an den Graphen \(G_{f}\) der Funktion \(f\).

Betrachtet man die Steigung einer Tangente an \(G_{f}\) in der Umgebung der Extrempunkte von \(G_{f}\), lässt sich Folgendes schlussfolgern:

• Der Graph \(G_{f'}\) der Ableitungsfunktion \(f'\) hat an den Stellen \(x = -1\) und \(x = 2\) jeweils eine einfache Nullstelle (waagrechte Tangente an \(G_{f}\), Vorzeichenwechsel von \(f'\)).
• \(G_{f'}\) verläuft für \(x \in \; ]-\infty;-1[\) oberhalb der \(x\)-Achse \((f'(x) > 0)\).
• \(G_{f'}\) verläuft für \(x \in \; ]-1;2[\) unterhalb der \(x\)-Achse \((f'(x) < 0)\).
• \(G_{f'}\) verläuft für \(x \in \; ]2;+\infty[\) oberhalb der \(x\)-Achse \((f'(x) > 0)\).

Die genannte Eigenschaften des Graphen \(G_{f'}\) der Ableitungsfunktion \(f'\) erfüllt ausschließlich Graph III.

Graph der zugehörigen Stammfunktion \(F\)

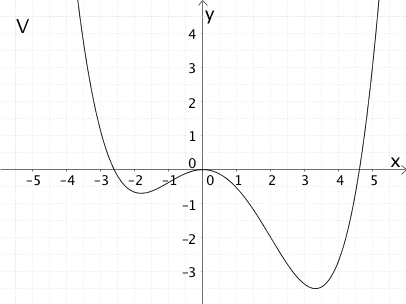
Graph V zeigt den Graphen einer zugehörigen Stammfunktion \(F\) von \(f\).

Begründung:

Um von einem Graphen \(G_{f}\) einer Funktion \(f\) auf den Graphen \(G_{F}\) einer zugehörigen Stammfunktion \(F\) zu schließen, werden insbesondere die Schnittpunkte von \(G_{f}\) mit der \(x\)-Achse (Nullstellen von \(f\)) und der Verlauf von \(G_{f}\) in deren Umgebung betrachtet.

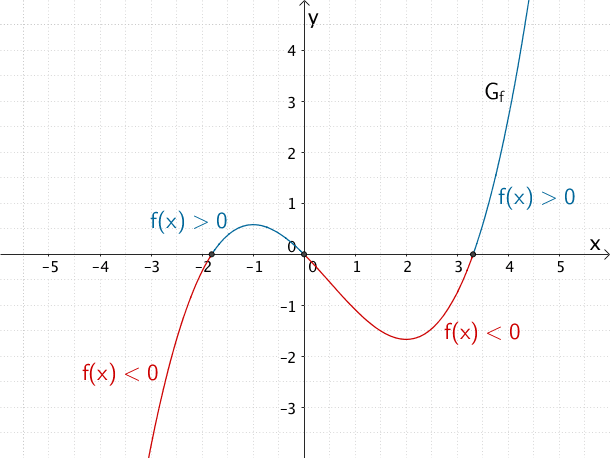
Der Graph \(G_{f}\) der Funktion \(f\) schneidet die \(x\)-Achse näherungsweise an den Stellen \(x \approx 1{,}8\), \(x \approx 0\) und \(x \approx 3{,}3\). Die Funktion \(f\) wechselt an diesen einfachen Nullstellen jeweils das Vorzeichen.

Gemäß der Definition einer Stammfunktion gilt:

\[F'(x) = f(x)\]

Mithilfe dieser Beziehung und dem Monotoniekriterium lässt sich näherungsweise die Lage der Extremstellen einer zugehörigen Stammfunktion \(F\) und die Art der Extrempunkte des Graphen \(G_{F}\) schlussfolgern:

\[\left. \begin{align*} &F'(x) < 0 \; \text{für} \; x \lesssim 1{,}8 \\[0.8em] &F'(1{,}8) \approx 0 \\[0.8em] &F'(x) > 0 \; \text{für} \; x \gtrsim 1{,}8 \end{align*} \right\} \enspace \Rightarrow \enspace \text{Tiefpunkt von} \;G_{F}\; \text{bei}\; x \approx 1{,}8\]

\[\left. \begin{align*} &F'(x) > 0 \; \text{für} \; x \lesssim 0 \\[0.8em] &F'(0) \approx 0 \\[0.8em] &F'(x) < 0 \; \text{für} \; x \gtrsim 0 \end{align*} \right\} \enspace \Rightarrow \enspace \text{Hochpunkt von} \;G_{F}\; \text{bei}\; x \approx 0\]

\[\left. \begin{align*} &F'(x) < 0 \; \text{für} \; x \lesssim 3{,}3 \\[0.8em] &F'(3{,}3) \approx 0 \\[0.8em] &F'(x) > 0 \; \text{für} \; x \gtrsim 3{,}3 \end{align*} \right\} \enspace \Rightarrow \enspace \text{Tiefpunkt von} \;G_{F}\; \text{bei}\; x \approx 3{,}3\]

Ausschließlich Graph V zeigt die genannten Etrempunkte an den Nullstellen der Funktion \(f\).