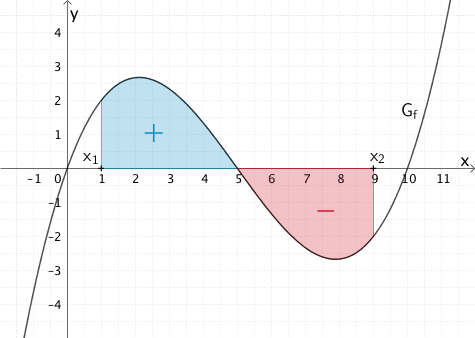
Im Folgenden wird die in \(\mathbb R\) definierte Funktion \(F_{1}\) mit \(\displaystyle F_{1}(x) = \int_{1}^{x} f(t) dt\) betrachtet.
\(F_{1}\) hat für \(0 \leq x \leq 10\) zwei ganzzahlige Nullstellen. Geben Sie diese an und begründen Sie Ihre Angabe.
(3 BE)
Lösung zu Teilaufgabe 1d
\[F_{1}(x) = \int_{1}^{x} f(t)dt; \; 0 \leq x \leq 10\]
Nullstelle einer Integralfunktion
Jede Integralfunktion \(\displaystyle I_{a} \colon x \mapsto \int_{a}^{x} f(t)\, dt\) besitzt an der unteren Integrationsgrenze \(x = a\) eine Nullstelle.
\[I_{a}(a) = \int_{a}^{a} f(t) \, dt = F(a) - F(a) = 0\]
\(F\) ist eine Stammfunktion von \(f\).
Die Integralfunktion \(F_{1}\) hat an der unteren Integrationsgrenze die ganzzahlige Nullstelle \(x_{1} = 1\).
Jeder Funktionswert \(F_{1}(x)\) mit \(0 \leq x \leq 10\) lässt sich als Flächenbilanz der Flächenstücke interpretieren, die \(G_{f}\) in einem betrachteten Intervall mit der \(x\)-Achse einschließt.