Die Kugel \(K\) mit dem Mittelpunkt \(M(-13|20|0)\) berührt die Ebene \(E\). Bestimmen Sie die Koordinaten des zugehörigen Berührpunkts \(F\) sowie den Kugelradius \(r\).
(zur Kontrolle: \(F(-5|4|2)\), \(r = 18\))
(6 BE)
Lösung zu Teilaufgabe c
Bestimmung der Koordinaten des Berührpunkts \(F\)
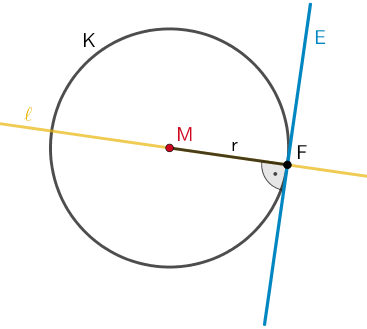
Im Berührpunkt \(F\) steht der Radius \(\mathbf{r}\) der Kugel \(K\) senkrecht auf der Ebene \(\textcolor{#0087c1}{\mathbf{E}}\).
Die Lotgerade \(\textcolor{#e9b509}{\mathbf{\ell}}\) zur Ebene \(\textcolor{}{\textcolor{#0087c1}{E}}\) durch den Mittelpunkt \(\textcolor{#cc071e}{M}\) der Kugel K schneidet die Ebene \(\textcolor{#0087c1}{\mathbf{E}}\) im Berührpunkt \(\mathbf{F}\) (Lotfußpunkt).
Der Normalenvektor der Ebene \(E\) ist ein Richtungsvektor der Lotgerade \(\ell\). Der Mittelpunkt \(M\) dient als Aufpunkt.
Gleichung der Lotgerade \(\ell\) aufstellen
\[\textcolor{#cc071e}{M(-13|20|0)}\]
\[E \colon 4x_{1} - 8x_{2} + x_{3} + 50 = 0 \enspace \Rightarrow \enspace \textcolor{#0087c1}{\overrightarrow{n}_{E} = \begin{pmatrix} 4 \\ -8 \\ 1 \end{pmatrix}}\]
Lotgerade auf eine Ebene
\[E\,\colon \overrightarrow{n}_E \circ (\overrightarrow{X} - \overrightarrow{A}) = 0; \quad P\,(p_1|p_2|p_3)\]
Die Lotgerade \(\ell\) mit \(P \in \ell\) auf eine Ebene \(E\) ist durch den Ortsvektor \(\overrightarrow{P}\) und den Normalenvektor \(\overrightarrow{n}_E\) eindeutig bestimmt:
\[\ell\,\colon \overrightarrow{X} = \overrightarrow{P} + \lambda \cdot \overrightarrow{n}_E; \; \lambda \in \mathbb R\]
\[\textcolor{#e9b509}{\ell} \colon \overrightarrow{X} = \textcolor{#cc071e}{\begin{pmatrix} -13 \\ 20 \\ 0 \end{pmatrix}} + \mu \cdot \textcolor{#0087c1}{\begin{pmatrix} 4 \\ -8 \\ 1 \end{pmatrix}}, \; \mu \in \mathbb R\]
Koordinaten des Berührpunkts \(F\) bestimmen
Hierfür werden die Koordinaten des Ortsvektors \(\overrightarrow{X}\) der Gleichung der Lotgeraden \(\ell\) in die Gleichung der Ebene \(E\) eingesetzt und diese nach dem Parameter \(\mu\) aufgelöst.
\[\begin{align*}\ell \colon \overrightarrow{X} &= \begin{pmatrix} -13 \\ 20 \\ 0 \end{pmatrix} + \mu \cdot \begin{pmatrix} 4 \\ -8 \\ 1 \end{pmatrix}, \; \mu \in \mathbb R \\[0.8em] \ell \colon \overrightarrow{X} &= \begin{pmatrix} \textcolor{#89ba17}{-13 + 4\mu} \\ \textcolor{#89ba17}{20 - 8\mu} \\ \textcolor{#89ba17}{\mu} \end{pmatrix}, \; \mu \in \mathbb R \end{align*}\]
\[E \colon 4x_{1} - 8x_{2} + x_{3} + 50 = 0\]
\[\begin{align*}\ell \cap E \colon 4 \cdot \textcolor{#89ba17}{(-13 + 4\mu)} - 8 \cdot \textcolor{#89ba17}{(20 - 8\mu)} + \textcolor{#89ba17}{\mu} + 50 &= 0 \\[0.8em] -52 + 16\mu - 160 + 64\mu + \mu + 50 &= 0 \\[0.8em] 81\mu - 162 &= 0 &&| + 162 \\[0.8em] 81\mu &= 162 &&| : 81 \\[0.8em] \mu &= 2 \end{align*}\]
Eingesetzt in die Gleichung der Lotgeraden \(\ell\) liefert der Parameterwert \(\textcolor{#89ba17}{\mu = 2}\) den Ortsvektor \(\overrightarrow{F}\) des Berührpunkts \(F\).
\[F \in \ell \colon \overrightarrow{F} = \begin{pmatrix} -13 \\ 20 \\ 0 \end{pmatrix} + \textcolor{#89ba17}{2} \cdot \begin{pmatrix} 4 \\ -8 \\ 1 \end{pmatrix} = \begin{pmatrix} -5 \\ 4 \\ 2 \end{pmatrix}\]
\[\Rightarrow \enspace F(-5|4|2)\]
Berechnung des Kugelradius \(r\)
\(M(-13|20|0)\), \(F(-5|4|2)\)
Betrag eines Vektors
\[ \vert \overrightarrow{a} \vert = \sqrt{\overrightarrow{a} \circ \overrightarrow{a}} = \sqrt{{a_1}^2 + {a_2}^2 + {a_3}^2}\]
(vgl. Merkhilfe)
\[\begin{align*}r &= \vert \overrightarrow{MF} \vert = \vert \overrightarrow{F} - \overrightarrow{M} \vert \\[0.8em] &= \left| \begin{pmatrix} -5 \\ 4 \\ 2 \end{pmatrix} - \begin{pmatrix} -13 \\ 20 \\ 0 \end{pmatrix} \right| = \left| \begin{pmatrix} 8 \\ -16 \\ 2 \end{pmatrix} \right| \\[0.8em] &= \sqrt{8^{2} + (-16)^{2} + 2^{2}} = \sqrt{324} = 18\end{align*}\]


