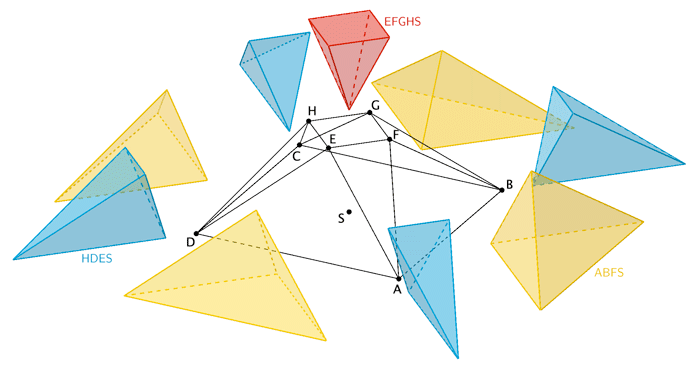
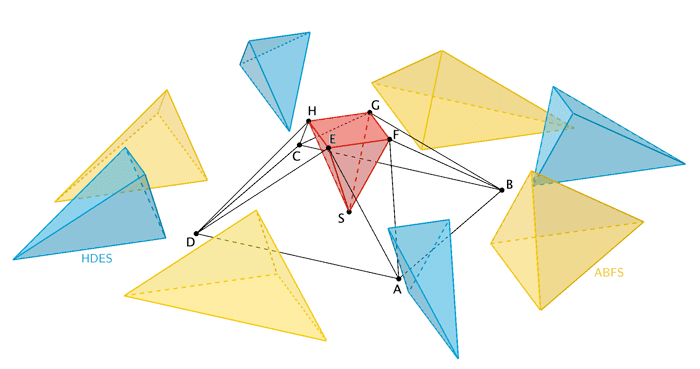
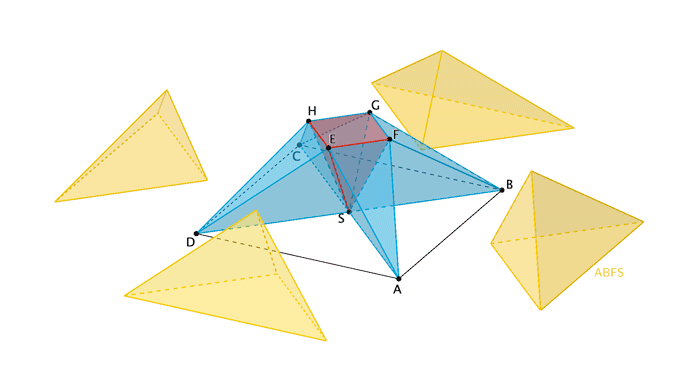
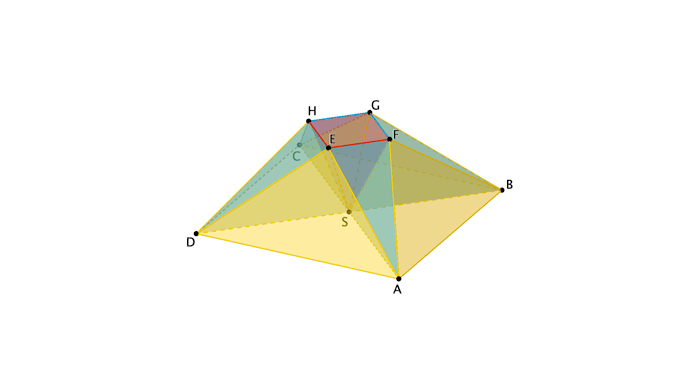
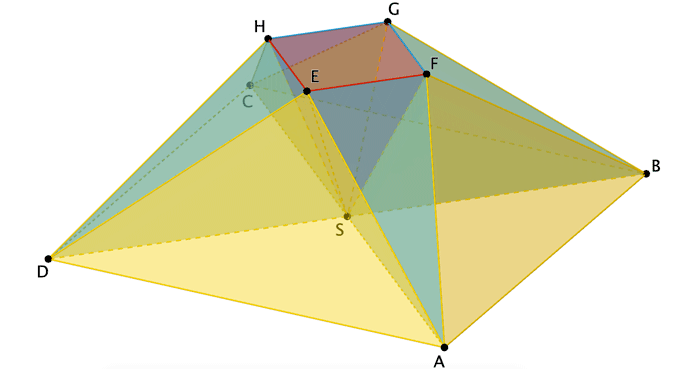
Der Körper kann in neun Pyramiden zerlegt werden, von denen jede kongruent zu genau einer der drei  Pyramiden \(ABFS\), \(HDES\) bzw. \(EFGHS\) ist (vgl. Abbildung 2). Die Pyramide \(ABFS\) hat das Volumen \(\sf{33\frac{1}{3}}\) und die Pyramide \(HDES\) hat das Volumen \(\sf{13\frac{1}{3}}\). Bestimmen Sie das Volumen des gesamten Körpers.

(4 BE)

Lösung zu Teilaufgabe f

• 
• 
• 
• 
• 

Der Körper besteht aus vier Pyramiden der Form \(\textcolor{#e9b509}{ABFS}\) und vier Pyramiden der Form \(\textcolor{#0087c1}{HDES}\) sowie der Pyramide \(\textcolor{#cc071e}{EFGHS}\).

Volumen der Pyramide \(\textcolor{#cc071e}{EFGHS}\) berechnen:

Die Grundfläche der Pyramide ist das Quadrat \(EFGH\) mit der Seitenlänge \(\overline{EF} = \sqrt{8}\) (vgl. Teilaufgabe d). Da die \(x_{3}\)-Koordinate der Punkte \(E\), \(F\), \(G\) und \(H\) jeweils 4 ist, und die Spitze \(S\) im Koordinatenursprung liegt, hat die Pyramide die Höhe \(h = 4\) (Abstand Spitze - Grundfläche).

\[\textcolor{#cc071e}{V_{EFGHS}} = \frac{1}{3} \cdot \overline{EF}^{2} \cdot h = \frac{1}{3} \cdot \left( \sqrt{8} \right)^{2} \cdot 4 = \frac{32}{3} = \textcolor{#cc071e}{10\frac{2}{3}}\]

Volumen des Körpers berechnen:

\(\textcolor{#e9b509}{V_{ABFS} = 33\frac{1}{3}}\), \(\textcolor{#0087c1}{V_{HDES} = 13\frac{1}{3}}\), \(\textcolor{#cc071e}{V_{EFGHS} = 10\frac{2}{3}}\)

\[\begin{align*} V_{\text{Körper}} &= 4 \cdot \textcolor{#e9b509}{V_{ABFS}} + 4 \cdot \textcolor{#0087c1}{V_{HDES}} + \textcolor{#cc071e}{V_{EFGHS}} \\[0.8em] &= 4 \cdot \textcolor{#e9b509}{33\frac{1}{3}} + 4 \cdot \textcolor{#0087c1}{13\frac{1}{3}} + \textcolor{#cc071e}{10\frac{2}{3}} \\[0.8em] &= 4 \cdot \frac{100}{3} + 4 \cdot \frac{40}{3} + \frac{32}{3} \\[0.8em] &= \frac{592}{3} = 197\frac{1}{3}\end{align*}\]