Das Aquarium wird vollständig mit Wasser gefüllt.

Berechnen Sie die größtmögliche Wassertiefe des Aquariums.

(2 BE)

Lösung zu Teilaufgabe 2d

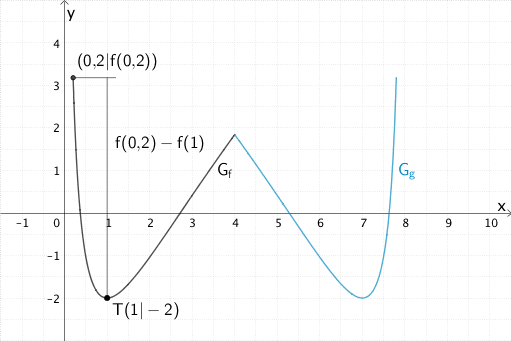
Die Kurve \(k\) enthält für \(0{,}2 \leq x \leq 4\) den Graphen \(G_{f}\). Der Punkt \((0{,}2|f(0{,}2))\) liegt somit auf der Wasseroberfläche des vollständig gefüllten Aquariums (vgl. Angabe Teilaufgabe 2c). Der Tiefpunkt \(T(1|-2)\) von \(G_{f}\) (vgl. Teilaufgabe 1a) beschreibt einen Punkt auf dem Beckengrund des Aquariums .

Somit lässt sich die größtmögliche Wassertiefe des Aquariums wie folgt berechnen:

\(f(x) = 2 \cdot \left( \left( \ln{x} \right)^{2} - 1 \right); \; 0{,}2 \leq x \leq 4\)

\[f(0{,}2) - f(1) = 2 \cdot \left( \left( \ln{0{,}2} \right)^{2} - 1 \right) - (-2) \approx 5{,}18\]

Die größtmögliche Wassertiefe des Aquarium beträgt ca. 5,18 Meter.