Nur zu dem Zeitpunkt, der im Modell durch \(x_{0}\) (vgl. Aufgabe 2b) beschrieben wird, nimmt die momentane Änderungsrate des Flächeninhalts des Algenteppichs ihren größten Wert an. Geben Sie eine besondere Eigenschaft des Graphen von \(A\) im Punkt \((x_{0}|A(x_{0}))\) an, die sich daraus folgern lässt, und begründen Sie Ihre Angabe.
(2 BE)
Lösung zu Teilaufgabe 2d
Der Punkt \((x_{0}|A(x_{0}))\) ist Wendepunkt des Graphen von \(A\).
Begründung (Kurzversion)
Da die erste Ableitung \(A'\) (momentane Änderungsrate) an der Stelle \(x_{0}\) ein Maximum hat (Hochpunkt von \(G_{A'}\)), hat die zweite Ableitung \(A''\) (Steigung von \(G_{A'}\)) an der Stelle \(x_{0}\) eine Nullstelle mit Vorzeichenwechsel. Folglich besitzt der Graph von \(A\) den Wendepunkt \((x_{0}|A(x_{0}))\).
Anwendung der Differetialrechnung:
Wendepunkt
Ist \(f''(x_0) = 0\) und wechselt \(f''\) an der Stelle \(x_0\) das Vorzeichen, so hat \(G_f\) an der Stelle \(x_0\) einen Wendepunkt.
(vgl. Merkhilfe)
Alternative:
Es muss \(f''(x_{0}) = 0\) und \(f'''(x_{0}) \neq 0\) gelten.
Ausführliche Begründung
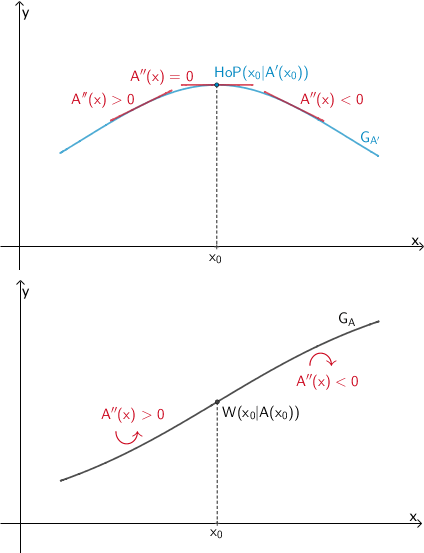
Schematische Darstellung: Graph von \(\textcolor{#0087c1}{A'}\) mit Hochpunkt \(\textcolor{#0087c1}{HoP(x_{0}|A'(x_{0}))}\) sowie Graph von \(A\) mit Wendepunkt \(W(x_{0}|A(x_{0})\)
Differentialquotient oder lokale bzw. momentane Änderungsrate
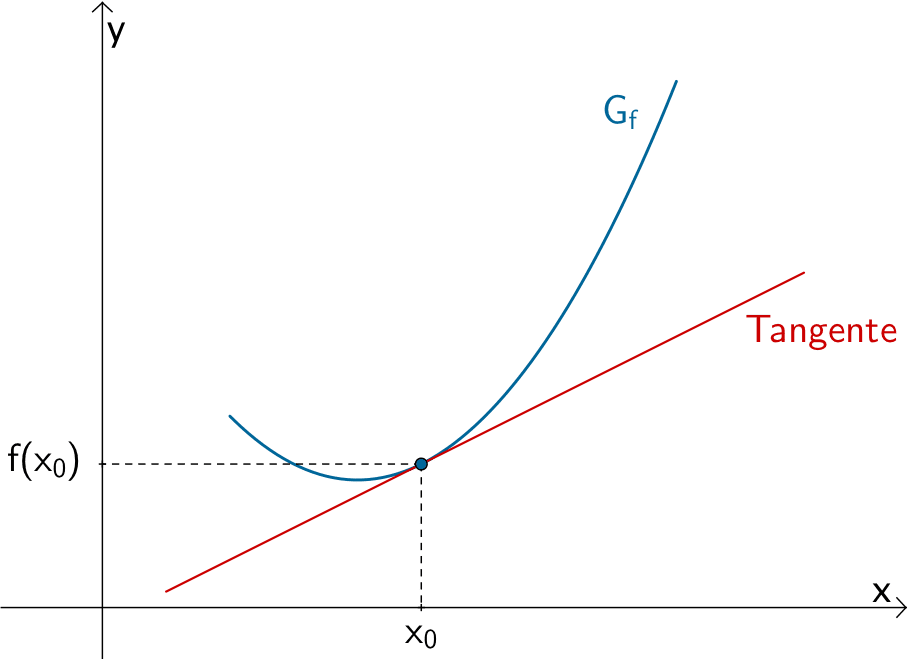
Der Differentialquotient oder die lokale bzw. momentane Änderungsrate \(m_{x_{0}} = \lim \limits_{x \, \to \, x_{0}} \dfrac{f(x) - f(x_{0})}{x - x_{0}}\) beschreibt den Grenzwert des Differenzenquotienten \(\dfrac{f(x) - f(x_{0})}{x - x_{0}}\) bei beliebig genauer Annäherung \(x \to x_{0}\) und damit die Steigung der Tangente an den Graphen der Funktion \(f\) an der Stelle \(x_{0}\).
Man nennt den Grenzwert \(m_{x_{0}}\) die Ableitung von \(f\) an der Stelle \(x_{0}\) und schreibt dafür \(f'(x_{0})\). Voraussetzung: Der Grenzwert existiert an der Stelle \(x_{0}\) und ist endlich.
\[f'(x_{0}) = \lim \limits_{x \, \to \, x_{0}} \dfrac{f(x) - f(x_{0})}{x - x_{0}}\]
(vgl. Merkhilfe)
Die erste Ableitung \(\textcolor{#0087c1}{A'}\) beschreibt die momentane Änderungsrate des Flächeninhalts des Algenteppichs. An der Stelle \(\mathbf{x_{0}}\) (vgl. Teilaufgabe 2b) ist die momentane Änderungsrate maximal (vgl. Angabe), also hat der Graph von \(\textcolor{#0087c1}{A'}\) den Hochpunkt \(\textcolor{#0087c1}{HoP(x_{0}|A'(x_{0}))}\).
Anwendung der Differetialrechnung:
Steigung \(m_{T}\) einer Tangente \(T\) an den Graphen einer Funktion \(f\) im Punkt \(P\,(\,x_0\,|\,f(x_0)\,)\)
\[m_{T} = f'(x_0)\]
(vgl. Merkhilfe)
Die Ableitung von \(\textcolor{#cc071e}{A'}\), d.h. die zweite Ableitung \(\textcolor{#cc071e}{A''}\), beschreibt die Steigung einer Tangente an den Graphen von \(\textcolor{#cc071e}{A'}\).
An der Stelle \(\mathbf{x_{0}}\) besitzt der Graph von \(\textcolor{#0087c1}{A'}\) eine waagrechte Tangente (Steigung ist Null). Somit gilt: \(\textcolor{#cc071e}{A''(x_{0}) = 0}.\)
Anwendung der Differentialrechnung:
Krümmungsverhalten von Funktionsgraphen
\(f''(x) < 0\) im Intervall \(I \quad \Longrightarrow \quad G_f\) ist in \(I\) rechtsgekrümmt.
\(f''(x) > 0\) im Intervall \(I \quad \Longrightarrow \quad G_f\) ist in \(I\) linksgekrümmt.
(vgl. Merkhilfe)
Im Hochpunkt von \(\textcolor{#0087c1}{G_{A'}}\) wechselt die Tangentensteigung von „positiv" nach „negativ". Folglich hat \(\textcolor{#cc071e}{A''}\) an der Stelle \(\mathbf{x_{0}}\) einen Vorzeichenwechsel von \(\textcolor{#cc071e}{+}\) nach \(\textcolor{#cc071e}{-}\). Das bedeutet, dass der Graph von \(\mathbf{A}\) an der Stelle \(\mathbf{x_{0}}\) das Krümmungsverhalten von „linksgekrümmt" \(\style{display: inline-block; transform:rotate(0.5turn);}{ \textcolor{#cc071e}{\curvearrowleft}}\) nach „rechtsgekrümmt" \(\textcolor{#cc071e}{\curvearrowright}\) ändert.
Anwendung der Differetialrechnung:
Wendepunkt
Ist \(f''(x_0) = 0\) und wechselt \(f''\) an der Stelle \(x_0\) das Vorzeichen, so hat \(G_f\) an der Stelle \(x_0\) einen Wendepunkt.
(vgl. Merkhilfe)
Alternative:
Es muss \(f''(x_{0}) = 0\) und \(f'''(x_{0}) \neq 0\) gelten.
Also besitzt der Graph von \(\mathbf{A}\) den Wendepunkt \(\mathbf{(x_{0}|A(x_{0}))}\).
\[\left. \begin{align*} &\textcolor{#cc071e}{A''(x) > 0} \enspace \text{für} \enspace x < x_{0} \\ &\textcolor{#cc071e}{A''(x_{0}) = 0} \\ &\textcolor{#cc071e}{A''(x) < 0} \enspace \text{für} \enspace x > x_{0} \end{align*} \right \} \enspace \Rightarrow \enspace \text{Wendepunkt} \; W(x_{0}|A_{0})\]


