Für genau einen Wert von \(a\) hat die Gerade \(g_{a}\) einen Schnittpunkt mit der \(x_{3}\)-Achse. Ermitteln Sie die Koordinaten dieses Schnittpunkts.
(3 BE)
Lösung zu Teilaufgabe 2b
\(g_{a} \colon \overrightarrow{X} = \begin{pmatrix} 2 \\ a - 4 \\ 4 \end{pmatrix} + \lambda \cdot \begin{pmatrix} 2 \\ -2 \\ 1 \end{pmatrix}, \; \lambda \in \mathbb R\) mit \(a \in \mathbb R\)
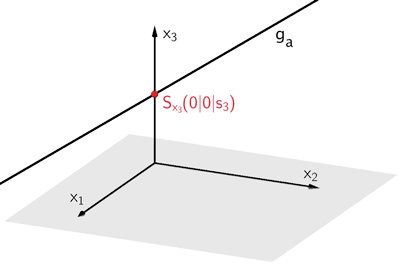
Die \(x_{1}\)- sowie die \(x_{2}\)-Koordinate des Schnittpunkts \(S_{x_{3}}\) einer Geraden \(g_{a}\) mit der \(x_{3}\)-Achse ist jeweils gleich Null: \(x_{1} = 0\), \(x_{2} = 0\).
Die \(x_{1}\)- und die \(x_{2}\)-Koordiante des Ortsvektors \(\overrightarrow{X} = \begin{pmatrix} x_{1} \\ x_{2} \\ x_{3} \end{pmatrix}\) der Gleichung einer Geraden \(g_{a}\) muss also gleich Null sein.
\[\begin{pmatrix} \textcolor{#cc071e}{0} \\ \textcolor{#0087c1}{0} \\ x_{3} \end{pmatrix} = \begin{pmatrix} \textcolor{#cc071e}{2} \\ \textcolor{#0087c1}{a - 4} \\ 4 \end{pmatrix} + \lambda \cdot \begin{pmatrix} \textcolor{#cc071e}{2} \\ \textcolor{#0087c1}{-2} \\ 1 \end{pmatrix}\]
Zeilenweise gelesen, ergeben die ersten beiden Zeilen der Vektorgleichung ein lineares Gleichungssystem für die zu bestimmenden Unbekannten \(\lambda\) und \(a\).
\[\Longrightarrow \quad \begin{cases} \;\, \textcolor{#cc071e}{\text{I} \quad 0 = 2 + \lambda \cdot 2} \quad \Longleftrightarrow \quad \lambda = -1 \\[0.8em] \textcolor{#0087c1}{\text{II} \quad 0 = a - 4 + \lambda \cdot (-2)} \end{cases}\]
\[\begin{align*} \lambda = -1 \; \text{in II} \colon \; 0 &= a - 4 + (-1) \cdot (-2) \\[0.8em] 0 &= a - 2 &&| + 2 \\[0.8em] 2 &= a \end{align*}\]
Mit \(\lambda = -1\) und \(a = 2\) folgt:
\[S_{x_{3}} \in g_{a} \colon \overrightarrow{S_{x_{3}}} = \begin{pmatrix} 2 \\ 2 - 4 \\ 4 \end{pmatrix} + (-1) \cdot \begin{pmatrix} 2 \\ -2 \\ 1 \end{pmatrix} = \begin{pmatrix} 0 \\ 0 \\ 3 \end{pmatrix}\]
\[\Longrightarrow \quad S_{x_{3}}(0|0|3)\]


