Betrachtet wird nun die Integralfunktion \(\displaystyle F \colon x \mapsto \int_{0}^{x} f(t)\,dt\) mit Definitionsbereich \(D_{F} = [-5;5]\).
Zeigen Sie mithilfe einer geometrischen Überlegung, dass \(F(5) = \frac{25}{4}\pi\) gilt.
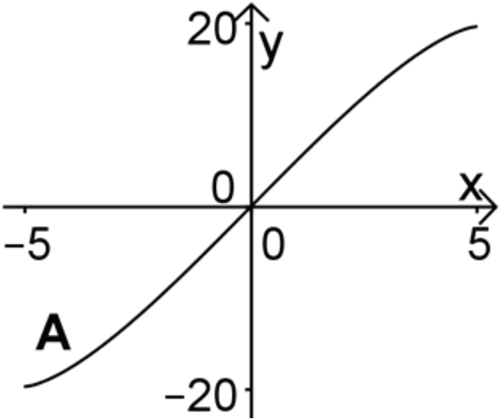
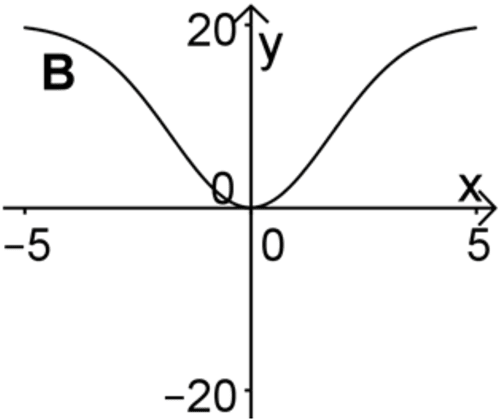
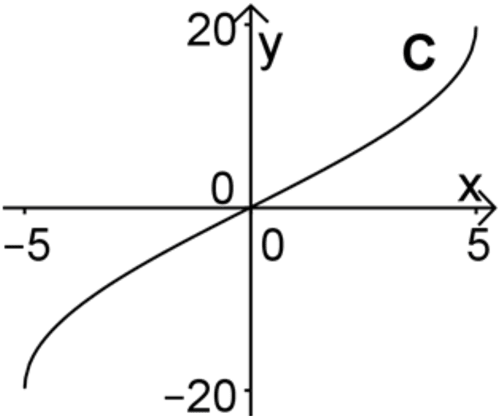
Einer der Graphen A, B und C ist der Graph von \(F\). Entscheiden Sie, welcher dies ist, und begründen Sie Ihre Entscheidung, indem Sie erklären, warum die beiden anderen Graphen nicht infrage kommen.
(5 BE)
Lösung zu Teilaufgabe 3b
\[F(x) = \int_{0}^{x} f(t)\, dt; \; D_{F} = [-5;5]\]
Nachweis, dass \(F(5) = \frac{25}{4}\pi\) gilt
\[F(5) = \int_{0}^{5} f(t)\, dt\]
Aus Teilaufgabe 3a ist bekannt, dass der Graph der Funktion \(f\) ein Halbkreis mit dem Mittelpunkt \(M(0|0)\) und dem Radius \(r = 5\) ist. Folglich ist der Funktionswert \(F(5)\) gleich der Maßzahl des Flächeninhalts des Viertelkreises, den der Graph der Funktion \(f\) im I. Quadranten mit den Koordinatenachsen einschließt.
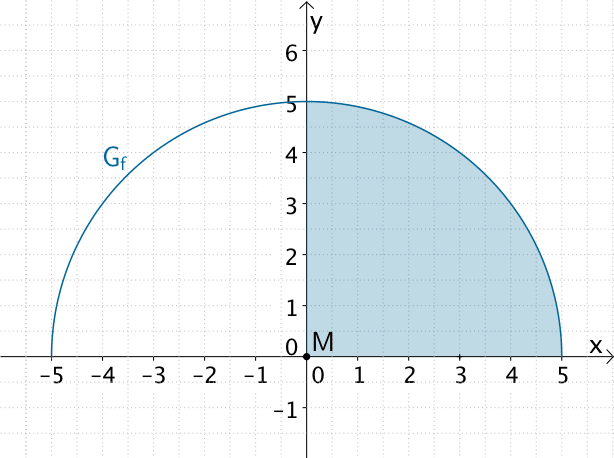
Flächeninhalt des Viertelkreises, den der Graph der Funktion \(f\) im I. Quadranten mit den Koordinatenachsen einschließt.
\[F(5) = \int_{0}^{5} f(t)\, dt = \frac{1}{4} \cdot r^{2} \cdot \pi = \frac{1}{4} \cdot 5^{5} \cdot \pi = \frac{25}{4}\pi\]
Zuordnung und Begründung, welcher der Graphen A, B und C der Graph von \(F\) ist
\[F(x) = \int_{0}^{x} f(t)\, dt; \; D_{F} = [-5;5]\]



Graph A ist der Graph der Integralfunktion \(F\).
Gemäß der Aufgabenstellung erfolgt die Begründung nach dem Ausschlussprinzip.
Begründung, weshalb Graph B nicht in Frage kommt
1. Möglichkeit: Verlauf des Graphen B für \(x \in [-5;0[\) betrachten

Graph B verläuft für \(x \in [-5;0[\) oberhalb der \(x\)-Achse.
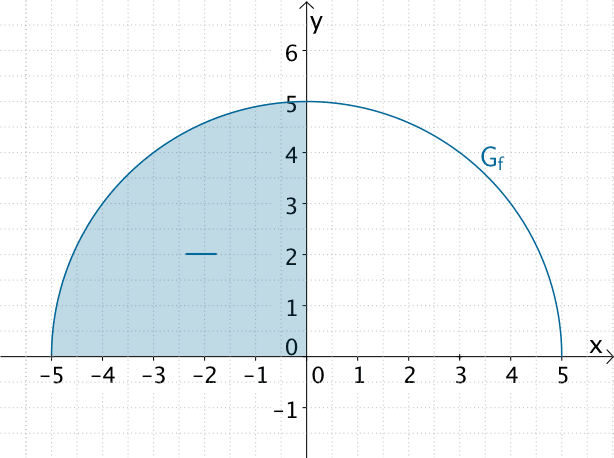
Für \(x \in [-5;0[\) ist der Wert der Integralfunktion \(F \colon x \mapsto \displaystyle \int_{0}^{x} f(t)\, dt\) negativ, da „nach links" integriert wird. Folglich muss der Graph der Integralfunktion \(F\) für \(x \in [-5;0[\) unterhalb der \(x\)-Achse verlaufen (und nicht oberhalb wie bei Graph B).
\(F(x) < 0\) für \(x \in [-5;0[\)
\(\Longrightarrow \quad\) Graph B ist nicht der Graph von \(F\).
2. Möglichkeit: Extrempunkt von Graph B betrachten

Graph B zeigt an der Stelle \(x = 0\) einen Extrempunkt.
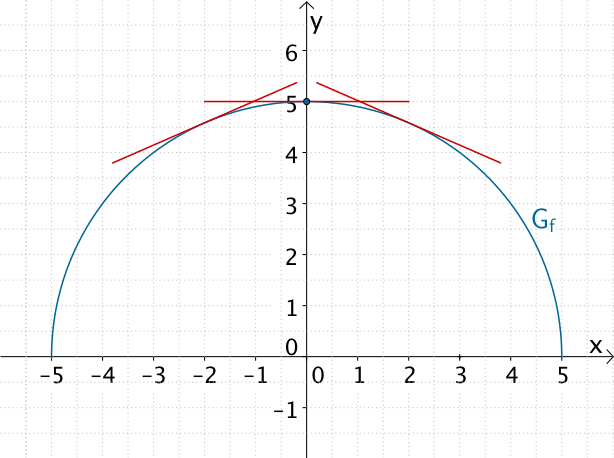
Der Graph der Funktion \(f\) hat an der Stelle \(x = 0\) einen Hochpunkt mit waagrechter Tangente (Steigung der Tangente ist gleich Null). In der Umgebung des Hochpunkts wechselt die Steigung einer Tangente an den Graphen der Funktion \(f\) das Vorzeichen von \(+\) nach \(-\). Die Ableitungsfunktion \(f'\) beschreibt die Steigung einer Tangente an \(G_{f}\).
\[\text{Hochpunkt}\; HoP(0|5) \enspace \Rightarrow \enspace \left\{ \begin{align*} &f'(x) > 0 \enspace \text{für} \enspace x < 0 \\[0.8em] &f'(0) = 0 \\[0.8em] &f'(x) < 0 \enspace \text{für} \enspace x > 0 \end{align*} \right.\]
Nach dem Hauptsatz der Differential- und Integralrechnung gilt:
Hauptsatz der Differential- und Integralrechnung (HDI)
Jede Integralfunktion \(\displaystyle I_{a} \colon x \mapsto \int_{a}^{x} f(t)\, dt\) einer stetigen Funktion \(f\) ist eine Stammfunktion von \(f\).
\[I_{a}(x) = \int_{a}^{x} f(t)\, dt \quad \Longrightarrow \quad I'_{a}(x) = f(x)\]
(vgl. Merkhilfe)
\[F''(x) = f'(x)\]
Folglich hat der Graph der Integralfunktion \(F\) an der Stelle \(x = 0\) einen Wendepunkt (und keinen Extrempunkt wie ihn Graph B zeigt).
Anwendung der Differetialrechnung:
Wendepunkt
Ist \(f''(x_0) = 0\) und wechselt \(f''\) an der Stelle \(x_0\) das Vorzeichen, so hat \(G_f\) an der Stelle \(x_0\) einen Wendepunkt.
(vgl. Merkhilfe)
Alternative:
Es muss \(f''(x_{0}) = 0\) und \(f'''(x_{0}) \neq 0\) gelten.
\[\left. \begin{align*} &F''(x) > 0 \enspace \text{für} \enspace x < 0 \\[0.8em] &F''(x) = 0 \\[0.8em] &F''(x) < 0 \enspace \text{für} \enspace x > 0 \end{align*} \right\} \enspace \Rightarrow \enspace \text{Wendepunkt} \; W(0|F(0))\]
Das Vorzeichen von \(F''\) informiert zudem über das Krümmungsverhalten der Integralfunktion \(F\):
Anwendung der Differentialrechnung:
Krümmungsverhalten von Funktionsgraphen
\(f''(x) < 0\) im Intervall \(I \quad \Longrightarrow \quad G_f\) ist in \(I\) rechtsgekrümmt.
\(f''(x) > 0\) im Intervall \(I \quad \Longrightarrow \quad G_f\) ist in \(I\) linksgekrümmt.
(vgl. Merkhilfe)
\(F''(x) > 0\) für \(x < 0\)
\(\Longrightarrow \quad\)\(G_{F}\) ist für \(x < 0\) linksgekrümmt.
\(F''(x) < 0\) für \(x > 0\)
\(\Longrightarrow \quad\)\(G_{F}\) ist für \(x > 0\) rechtsgekrümmt.
\(\Longrightarrow \quad\) Graph B ist nicht der Graph von \(F\).
Begründung, weshalb Graph C nicht in Frage kommt
1. Möglichkeit: Krümungsverhalten von Graph C betrachten

Graph C ist für \(x \in [-5;0[\) rechtsgekrümmt und für \(x \in ]0;5]\) linksgekrümmt.
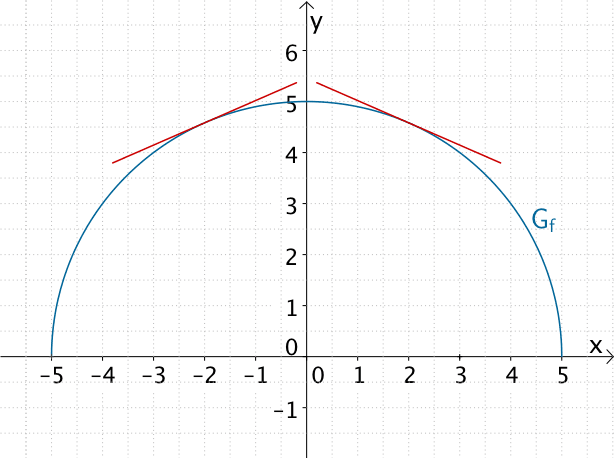
Die Steigung einer Tangente an den Graphen der Funktion \(f\) ist für \(x < 0\) positiv und für \(x > 0\) negativ. Die Ableitungsfunktion \(f'\) beschreibt die Steigung einer Tangente an \(G_{f}\).
\(f'(x) > 0\) für \(x < 0\)
\(f'(x) < 0\) für \(x > 0\)
Nach dem Hauptsatz der Differential- und Integralrechnung gilt:
Hauptsatz der Differential- und Integralrechnung (HDI)
Jede Integralfunktion \(\displaystyle I_{a} \colon x \mapsto \int_{a}^{x} f(t)\, dt\) einer stetigen Funktion \(f\) ist eine Stammfunktion von \(f\).
\[I_{a}(x) = \int_{a}^{x} f(t)\, dt \quad \Longrightarrow \quad I'_{a}(x) = f(x)\]
(vgl. Merkhilfe)
\[F''(x) = f'(x)\]
Damit lässt sich für das Krümmungsverhalten der Integralfunktion \(F\) schlussfolgern:
Anwendung der Differentialrechnung:
Krümmungsverhalten von Funktionsgraphen
\(f''(x) < 0\) im Intervall \(I \quad \Longrightarrow \quad G_f\) ist in \(I\) rechtsgekrümmt.
\(f''(x) > 0\) im Intervall \(I \quad \Longrightarrow \quad G_f\) ist in \(I\) linksgekrümmt.
(vgl. Merkhilfe)
\(F''(x) > 0\) für \(x < 0\)
\(\Longrightarrow \quad\)\(G_{F}\) ist für \(x < 0\) linksgekrümmt.
\(F''(x) < 0\) für \(x > 0\)
\(\Longrightarrow \quad\)\(G_{F}\) ist für \(x > 0\) rechtsgekrümmt.
\(\Longrightarrow \quad\) Graph C ist nicht der Graph von \(F\).
2. Möglichkeit: Verhalten von Graph C an den Definitionsrändern betrachten

Für \(x \to -5\) und \(x \to 5\) geht die Steigung einer Tangente an Graph C gegen \(+\infty\).
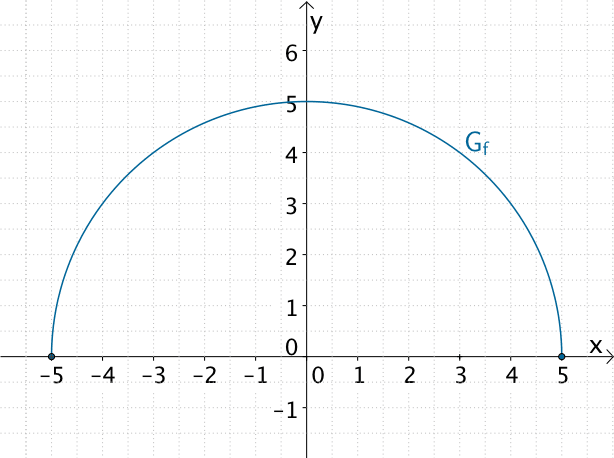
Der Graph der Funktion \(f \colon x \mapsto \sqrt{25 - x^{2}}\) besitzt an den Rändern seines Definitionsbereichs \(D_{f} = [-5;5]\) Nullstellen.
\[f(-5) = 0\]
\[f(5) = 0\]
Nach dem Hauptsatz der Differential- und Integralrechnung gilt:
Hauptsatz der Differential- und Integralrechnung (HDI)
Jede Integralfunktion \(\displaystyle I_{a} \colon x \mapsto \int_{a}^{x} f(t)\, dt\) einer stetigen Funktion \(f\) ist eine Stammfunktion von \(f\).
\[I_{a}(x) = \int_{a}^{x} f(t)\, dt \quad \Longrightarrow \quad I'_{a}(x) = f(x)\]
(vgl. Merkhilfe)
\[F'(x) = f(x)\]
Somit gilt:
\[F'(-5) = f(-5) = 0\]
\[F'(5) = f(5) = 0\]
Die Ableitungsfunktion \(F'\) beschreibt die Steigung einer Tangente an den Graphen der Integralfunktion \(F\). Folglich muss die Steigung einer Tangente an \(G_{F}\) an den Rändern des Definitionsbereichs \(D_{F} = [-5;5]\) gleich Null sein. Das heißt, \(G_{F}\) muss an den Rändern des Definitionsbereichs ein waagrechte Tangente haben (und keine senkrechte Tangente wie bei Graph C).
\(\Longrightarrow \quad\) Graph C ist nicht der Graph von \(F\).
Schlussfolgerung
Nach dem Ausschlussprinzip ist Graph A der Graph von \(F\).

