Alle Eckpunkte des Oktaeders liegen auf einer Kugel. Geben Sie eine Gleichung dieser Kugel an.
Berechnen Sie den Anteil des Oktaedervolumens am Kugelvolumen.
(3 BE)
Lösung zu Teilaufgabe f
Kugelgleichung aufstellen, Volumen einer Kugel
Gleichung der Kugel auf der alle Eckpunkte des Oktaeders liegen
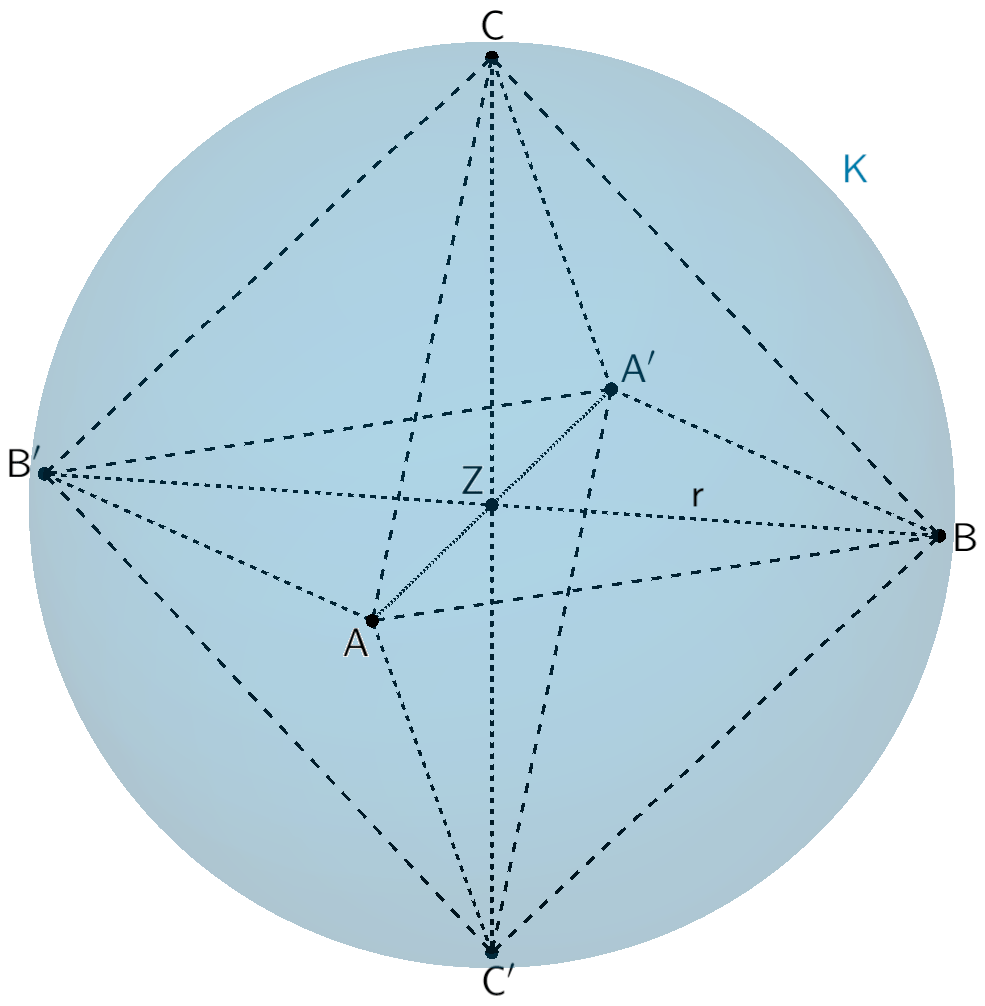
Der Punkt \(Z\) ist Symmetriezentrum des Okaeders \(ABA'B'CC'\) (vgl. Teilaufgabe b,d). Die Strecken \([AA']\), \([BB']\) und \([CC']\) schneiden sich im Punkt \(Z\) und beschreiben jeweils den Durchmesser der Kugel \(K\), auf der alle Eckpunkte des Oktaeders liegen. Folglich ist der Punkt \(Z\) der Mittelpunkt der Kugel \(K\) mit dem Radius \(r = \overline{AZ} = \overline{BZ} = \overline{CZ}\).
Radius \(r\) der Kugel berechnen:
Ggf. ist die Länge der Strecke \([AZ]\), \([BZ]\) oder \([CZ]\) aus einer der Teilaufgaben c,d oder e bereits bekannt. Andernfalls berechnet man die Länge einer dieser Strecken.
\(A(6|3|3)\), \(B(3|6|3)\), \(C(3|3|6)\), \(Z(3|3|3)\)
\[\begin{align*}\overline{AZ} &= \vert \overrightarrow{AZ} \vert \\[0.8em] &= \vert \overrightarrow{Z} - \overrightarrow{A} \vert \\[0.8em] &= \left| \begin{pmatrix} 3 \\ 3 \\ 3 \end{pmatrix} - \begin{pmatrix} 6 \\ 3 \\ 3 \end{pmatrix} \right| \\[0.8em] &= \left| \begin{pmatrix} -3 \\ 0 \\ 0 \end{pmatrix} \right| \\[0.8em] &= \sqrt{(-3)^{2} + 0^{2} + 0^{2}} \\[0.8em] &= \sqrt{9} \\[0.8em] &= 3 \end{align*}\]
\[\begin{align*}\overline{BZ} &= \vert \overrightarrow{BZ} \vert \\[0.8em] &= \vert \overrightarrow{Z} - \overrightarrow{B} \vert \\[0.8em] &= \left| \begin{pmatrix} 3 \\ 3 \\ 3 \end{pmatrix} - \begin{pmatrix} 3 \\ 6 \\ 3 \end{pmatrix} \right| \\[0.8em] &= \left| \begin{pmatrix} 0 \\ -3 \\ 0 \end{pmatrix} \right| \\[0.8em] &= \sqrt{0^{2} + (-3)^{2} + 0^{2}} \\[0.8em] &= \sqrt{9} \\[0.8em] &= 3 \end{align*}\]
\[\begin{align*}\overline{CZ} &= \vert \overrightarrow{CZ} \vert \\[0.8em] &= \vert \overrightarrow{Z} - \overrightarrow{C} \vert \\[0.8em] &= \left| \begin{pmatrix} 3 \\ 3 \\ 3 \end{pmatrix} - \begin{pmatrix} 3 \\ 3 \\ 6 \end{pmatrix} \right| \\[0.8em] &= \left| \begin{pmatrix} 0 \\ 0 \\ -3 \end{pmatrix} \right| \\[0.8em] &= \sqrt{0^{2} + 0^{2} + (-3)^{2}} \\[0.8em] &= \sqrt{9} \\[0.8em] &= 3 \end{align*}\]
\[\Longrightarrow \quad r = \overline{AZ} = \overline{BZ} = \overline{CZ} = 3\]
Gleichung der Kugel \(K\) aufstellen:
Kugelgleichung
Eine Kugel mit dem Mittelpunkt \(M(m_{1}|m_{2}|m_{3})\) und dem Radius \(r\) wird beschrieben durch:
Vektordarstellung
\[(\overrightarrow{X} - \overrightarrow{M})^{2} = r^{2}\]
Koordinatendarstellung
\[(x_{1} - m_{1})^{2} + (x_{2} - m_{2})^{2} + (x_{3} - m_{3})^{2} = r^{2}\]
\(Z(3|3|3)\), \(r = 3\)
Vektordarstellung:
\[K \colon \left( \overrightarrow{X} - \overrightarrow{Z} \right)^{2} = r^{2}\]
\[K \colon \left[ \begin{pmatrix} x_{1} \\ x_{2} \\ x_{3} \end{pmatrix} - \begin{pmatrix} 3 \\ 3 \\ 3 \end{pmatrix} \right]^{2} = 9\]
Koordinatendarstellung (vgl. Merkhilfe):
\[K \colon (x_{1} - z_{1})^{2} + (x_{2} - z_{2})^{2} + (x_{3} - z_{3})^{2} = r^{2}\]
\[K \colon (x_{1} - 3)^{2} + (x_{2} - 3)^{2} + (x_{3} - 3)^{2} = 9\]
Anteil des Oktaedervolumens am Kugelvolumen
Volumen der Kugel \(K\) berechnen (vgl. Merkhilfe):
\(r = 3\)
\[V_{K} = \frac{4}{3} r^{3} \pi = \frac{4}{3} \cdot 3^{3} \cdot \pi = 36\pi\]
Anteil des Oktaedervolumnes am Kugelvolumen berechnen:
\(V_{\text{Oktaeder}} = 36\) (vgl. Teilaufgabe d)
\[\frac{V_{\text{Oktaeder}}}{V_{K}} = \frac{\cancel{36}}{\cancel{36}\pi} = \frac{1}{\pi} \approx 0{,}318 = 31{,}8\,\%\]
Der Anteil des Oktaedervolumens am Kugelvolumen beträgt ca. 31,8 %.

